Space Launch System

The Space Launch System (abbreviated as SLS) is an American super heavy-lift expendable launch vehicle under development by NASA since 2011. The first launch, designated Artemis 1, is scheduled for 14 November 2022 from Kennedy Space Center. It replaces the Ares I and Ares V launch vehicles, which were cancelled along with the rest of the Constellation program, a previous program aimed to return to the Moon. The SLS is intended to become the successor to the retired Saturn V, and the primary launch vehicle of NASA's deep space exploration plans through the 2020s. Crewed lunar flights are planned as part of the Artemis program, leading to a possible human mission to Mars. The SLS is being developed in three major phases with increasing capabilities: Block 1, Block 1B, and Block 2. As of August 2019, SLS Block 1 launch vehicles are to launch the first three Artemis missions and five subsequent SLS flights are planned to use Block 1B, after which all flights will use Block 2.

Space Launch System

SLS Block 1 with the Orion spacecraft on pad 39B ahead of launch.

Function: Super heavy-lift launch vehicle
Manufacturer: Aerojet Rocketdyne, Northrop Grumman, Boeing, United Launch Alliance
Country of origin: United States
Project cost: US$23.011 billion (inflation adjusted, through 2021)
Cost per launch: Over US$2 billion excluding development (estimate)
Cost per year: US$2.555 billion for FY 2021

Size

Height:
- Block 1 Crew: 322 ft (98 m)
- Block 2 Cargo: 365 ft (111 m)
Diameter: 27.6 ft (8.4 m), Core stage
Stages: 2

Capacity

Payload to LEO

Mass:
- Block 1: 209,000 lb (95 t)
- Block 1B: 231,000 lb (105 t)
- Block 2: 290,000 lb (130 t)

Payload to trans-lunar injection

Mass:
- Block 1: > 59,500 lb (27 t)
- Block 1B Crew: 83,700 lb (38 t)
- Block 1B Cargo: 92,500 lb (42 t)
- Block 2 Crew: > 94,700 lb (43 t)
- Block 2 Cargo: > 101,400 lb (46 t)

Associated rockets

Comparable:
- Ares V
- Energia
- N1
- Saturn V
- Space Shuttle
- Falcon Heavy
- Starship
- Long March 9

Launch history

Status: Awaiting first launch at LC-39B
Launch sites: Kennedy Space Center, LC-39B
Total launches: 0
First flight: 14 November 2022
People or cargo transported: Orion

The SLS is planned to launch the Orion spacecraft as part of the Artemis program, making use of the ground operations and launch facilities at NASA's Kennedy Space Center in Florida. Artemis is projected to use at most one SLS each year until at least 2030. SLS will launch from LC-39B at the Kennedy Space Center.

The first launch was originally mandated by Congress for December 2016, but it has been delayed by almost six years to the original six-year schedule.

After the first four Artemis missions, NASA plans to transfer production and launching of the Space Launch System to Deep Space Transport LLC, a joint venture between Boeing and Northrop Grumman.

Description

The SLS is a Space Shuttle-derived launch vehicle. The first stage of the rocket is powered by one central core stage and two outboard solid rocket boosters. All SLS Blocks share a common core stage design, while they differ in their upper stages and boosters.

Core stage

Together with the solid rocket boosters, the core stage is responsible for propelling the upper stage and payload out of the atmosphere and accelerating up to almost orbital velocity. It contains the liquid hydrogen fuel and liquid oxygen oxidizer tanks for the ascent phase, the forward and aft solid rocket booster attach points, avionics, and the Main Propulsion System (MPS). The MPS is responsible for supplying the four RS-25 engines with fuel and oxidizer, gimballing the engines using hydraulic actuators, and pressurizing the propellant tanks via autogenous pressurization. The core stage provides approximately 25% of the vehicle's thrust at liftoff. The stage is 213 ft (65 m) long by 28 ft (8.4 m) in diameter and is both structurally and visually similar to the Space Shuttle external tank. The first four flights will each use and expend four of the remaining sixteen RS-25D engines previously flown on Space Shuttle missions. Aerojet Rocketdyne modifies these engines with modernized engine controllers, higher throttle limits, as well as insulation for the high temperatures the engine section will experience due to their position adjacent to the solid rocket boosters. Later flights will switch to a RS-25 variant optimized for expended use, the RS-25E, which will lower per-engine costs by over 30%. The thrust of each RS-25D engine has been increased from 492,000 lbf (2,188 kN), as on the Space Shuttle, to 513,000 lbf (2,281 kN) on the sixteen modernized engines. The RS-25E will further increase per-engine thrust to 522,000 lbf (2,321 kN).

Boosters

Blocks 1 and 1B of the SLS are planned to use two five-segment solid rocket boosters. These solid rocket boosters use casing segments that were flown on Shuttle missions as parts of the four-segment Space Shuttle Solid Rocket Boosters. They possess an additional center segment, new avionics, and lighter insulation, but lack a parachute recovery system. The propellants for the solid rocket boosters are aluminum powder, which is very reactive, and ammonium perchlorate, a powerful oxidizer. They are held together by a binder, polybutadiene acrylonitrile (PBAN). The mixture has the consistency of a rubber eraser and is packed into each segment. The five-segment solid rocket boosters provide approximately 25% more total impulse than the Shuttle Solid Rocket Boosters, but will not be recovered after use.

The stock of SLS Block 1 to 1B boosters is limited by the number of casings left over from the Shuttle program, which allows for eight flights of the SLS. On 2 March 2019, the Booster Obsolescence and Life Extension program was announced. This program will develop new solid rocket boosters, to be built by Northrop Grumman Space Systems, for further SLS flights, marking the beginning of Block 2. These boosters will be derived from the composite-casing solid rocket boosters then in development for the canceled OmegA launch vehicle, and are projected to increase Block 2's payload to 290,000 lb (130 t) to LEO and at least 101,000 lb (46 t) to trans-lunar injection. As of July 2021, the BOLE program is under heavy development, with first firing expected in 2024.

Upper stages

The Interim Cryogenic Propulsion Stage (ICPS) is planned to fly on Artemis 1, 2, and 3 as the upper stage of SLS Block 1. It is a stretched and human-rated Delta IV 16 ft (5 m) Delta Cryogenic Second Stage powered by a single RL10 engine. The first ICPS will use the RL10B-2 variant, while the second and third ICPS will use the RL10C-2 variant. Block 1 is intended to be capable of lifting 209,000 lb (95 t) to low Earth orbit (LEO) in this configuration, including the weight of the ICPS as part of the payload. At the time of SLS core stage separation, Artemis 1 will be travelling on an initial 1,806 by 30 km (1,122 by 19 mi) suborbital trajectory. This trajectory will ensure safe disposal of the core stage. ICPS will then perform orbital insertion and a subsequent translunar injection burn to send Orion towards the Moon. The ICPS will be human-rated for the crewed Artemis 2 and 3 flights.

The Exploration Upper Stage (EUS) is planned to fly on Artemis 4. The EUS will complete the SLS ascent phase and then re-ignite to send its payload to destinations beyond LEO. It is expected to be used by Block 1B and Block 2. The EUS shares the core stage diameter of 8.4 meters, and will be powered by four RL10C-3 engines. It will eventually be upgraded to use four improved RL10C-X engines. As of March 2022, Boeing is developing a new composite-based fuel tank for the EUS that would increase Block 1B's overall payload mass capacity to TLI by 30 percent. The improved upper stage was originally named the Dual Use Upper Stage (DUUS, pronounced "duce") but was later renamed the Exploration Upper Stage (EUS).

Block variants

Development

Funding

During the joint Senate-NASA presentation in September 2011, it was stated that the SLS program had a projected development cost of US$18 billion through 2017, with $10 billion for the SLS rocket, $6 billion for the Orion spacecraft, and $2 billion for upgrades to the launch pad and other facilities at Kennedy Space Center. These costs and schedules were considered optimistic in an independent 2011 cost assessment report by Booz Allen Hamilton for NASA. An internal 2011 NASA document estimated the cost of the program through 2025 to total at least $41 billion for four 209,000 lb (95 t) launches (1 uncrewed, 3 crewed), with the 290,000 lb (130 t) version ready no earlier than 2030. The Human Exploration Framework Team estimated unit costs for Block 0 at $1.6 billion and Block 1 at $1.86 billion in 2010. However, since these estimates were made the Block 0 SLS vehicle was dropped in late 2011, and the design was not completed.

In September 2012, an SLS deputy project manager stated that $500 million is a reasonable target average cost per flight for the SLS program. In 2013, the Space Review estimated the cost per launch at $5 billion, depending on the rate of launches. NASA announced in 2013 that the European Space Agency will build the Orion service module. In August 2014, as the SLS program passed its Key Decision Point C review and entered full development, costs from February 2014 until its planned launch in September 2018 were estimated at $7.021 billion. Ground systems modifications and construction would require an additional $1.8 billion over the same time.

In October 2018, NASA's Inspector General reported that the Boeing core stage contract had made up 40% of the $11.9 billion spent on the SLS as of August 2018. By 2021, core stages were expected to have cost $8.9 billion, twice the initially planned amount. In December 2018, NASA estimated that yearly budgets for the SLS will range from $2.1 to $2.3 billion between 2019 and 2023.

In March 2019, the Trump administration released its Fiscal Year 2020 Budget Request for NASA. This budget did not include any money for the Block 1B and Block 2 variants of SLS. It was therefore uncertain whether these future variants of SLS will be developed, but congressional action restored this funding in the passed budget. Several launches previously planned for the SLS Block 1B are expected to fly on commercial launcher vehicles such as Falcon Heavy, New Glenn, and Vulcan. However, the request for a budget increase of $1.6 billion towards SLS, Orion, and crewed landers along with the launch manifest seem to indicate support of the development of Block 1B, debuting Artemis 3. An uncrewed Block 1B is planned to launch the Lunar Surface Asset in 2028, the first lunar outpost of the Artemis program.

For fiscal years 2011 through 2021, the SLS program had expended funding totaling $21.209 billion in nominal dollars. This is equivalent to $23.011 billion in 2021 dollars using the NASA New Start Inflation Indices.

On top of this, the costs to assemble, integrate, prepare and launch the SLS and its payloads are funded separately under Exploration Ground Systems, currently at about $600 million per year, and anticipated to stay there through at least the first four launches of SLS. Payloads that launch on SLS, such as the Orion crew capsule, are similarly accounted separately from SLS. Predecessor programs contributed development to SLS, such as the Ares V Cargo Launch Vehicle, funded from 2008 to 2010, a total of $70 million, and Ares I Crew Launch Vehicle, funded from 2006 to 2010, a total of $4.8 billion in development that included the 5-segment Solid Rocket Boosters that will be used on the SLS.

Programs that are included under the above SLS cost table include the interim Upper Stage for the SLS, the Interim Cryogenic Propulsion Stage (ICPS), which includes a $412 million contract.

Also included in the above SLS cost table are the costs of developing the Exploration Upper Stage:

Estimates of the per launch costs for the SLS have varied widely, partly due to uncertainty over how much the program will expend during development and testing before the operational launches begin, and partly due to various agencies using differing cost measures; but also based on differing purposes for which the cost estimates were developed. For example, a marginal cost per one additional launch ignores the development and annual recurring fixed costs, whereas a total cost per launch includes recurring costs but excludes development.

There are no official NASA estimates for how much the SLS will cost per launch, nor for the SLS program annual recurring costs once operational. Cost per launch is not a straightforward figure to estimate as it depends heavily on how many launches occur per year. For example, similarly, the Space Shuttle was estimated, in 2012 dollars, to cost $576 million per launch had it been able to achieve 7 launches per year, while the marginal cost of adding a single additional launch in a given year was estimated to be less than half of that, at just $252 million of marginal cost. However, at the rate that it flew, the final cost was $1.64 billion per Space Shuttle launch, including development.

NASA associate administrator William H. Gerstenmaier said in 2017 that there would be no official per flight cost estimates of any variety provided by NASA for the SLS. Other bodies, such as the Government Accountability Office (GAO), the NASA Office of Inspector General, the Senate Appropriations Committee, and the White House Office of Management and Budget have put out cost per launch figures, however. Several internal NASA programs and project concept study reports have released proposed budgets that include future SLS launches. For example, a concept study report for a space telescope stated it was advised by NASA HQ in 2019 to budget $500 million for an SLS launch in 2035. Another study in 2019 also proposing a space telescope assumed a budget for their launch of $650 million in current-day dollars, or $925 million for when the launch would occur, also in the "mid-2030s".

Europa Clipper is a NASA scientific mission that was initially required by Congress to launch on the SLS. Oversight bodies both internal and external to NASA disagreed with this requirement. First, NASA's Inspector General office published a report in May 2019 that stated Europa Clipper would need to give up $876 million for the "marginal cost" of its SLS launch. Then, an addendum to the letter published in August 2019 increased the estimate and stated that switching to a commercial rocket would save over $1 billion. However, those savings may have included a portion of costs related to the delay in launch schedule; a commercial alternative could launch earlier than SLS.

A JCL (Joint Cost and Schedule Confidence Level) analysis cited in that letter put the cost savings at $700 million, with the SLS at $1.05 billion per launch and the commercial alternative at $350 million. Finally, a letter from the White House Office of Management and Budget (OMB) to the Senate Appropriations Committee in October 2019 revealed that SLS's total cost to the taxpayer was estimated at "over $2 billion" per launch after development is complete; said development has cost $23 billion in 2021 dollars. The letter suggested Congress remove this requirement, agreeing the NASA Inspector General, adding that using a commercial launch vehicle for Europa Clipper instead of the SLS would save $1.5 billion overall. NASA did not deny this $2 billion cost of launch and an agency spokesperson stated it "is working to bring down the cost of a single SLS launch in a given year as the agency continues negotiations with Boeing on the long-term production contract and efforts to finalize contracts and costs for other elements of the rocket".

This OMB figure is dependent on the rate of construction, so building more SLS rockets faster could decrease the per-unit cost. For example, Exploration Ground Systems – whose only role is to support, assemble, integrate, and launch SLS – has separately budgeted fixed costs of $600 million per year on facilities, spread across however many rockets launch that year. Then, in December 2019, NASA Administrator Jim Bridenstine shared informally that he disagrees with the $2 billion figure since the marginal cost of an SLS launch should decrease after the first few, and is expected to end up around $800 million to $900 million, although contract negotiations were only just beginning for those later cores.

Then, in July 2021, NASA announced that instead of SLS, a SpaceX Falcon Heavy would be used to launch Europa Clipper. This was done for technical reasons unrelated to cost, and the total cost savings was estimated at US$2 billion.

In November 2021, a new NASA Office of Inspector General audit was released, which estimated that, at least for the first four launches of SLS, the per-launch production and operating costs would be $2.2 billion for SLS, plus $568 million for Exploration Ground Systems. Additionally, since the first four missions are under the Artemis program, the payload would cost $1 billion for Orion and $300 million for the ESA service module.

Early plans

The SLS was created by an act of Congress in the "NASA Authorization Act of 2010", Public Law 111–267, in which NASA was directed to create a system for launching payloads and crew into space that would replace the capabilities lost with the retirement of the Space Shuttle. The act set out certain goals, such as being able to lift 130 tons or more of payload into low earth orbit, a target date of December 31, 2016 for the system to be fully operational, and a directive to use "to the extent practicable" existing components, hardware, and workforce from the Space Shuttle and from Ares I. On 14 September 2011, NASA announced their plan to meet these requirements: the design for the SLS, with the Orion spacecraft as payload.

The SLS has considered several future development routes of potential launch configurations, with the planned evolution of the blocks of the rocket having been modified many times. Many options, all of which just needed to meet the congressionally mandated payload minimums, were considered, including a Block 0 variant with three main engines, a variant with five main engines, a Block 1A variant with upgraded boosters instead of the improved second stage, and a Block 2 with five main engines plus the Earth Departure Stage, with up to three J-2X engines.

In the initial announcement of the design of the SLS, NASA also announced an "Advanced Booster Competition", to select which boosters would be used on Block 2 of the SLS. Several companies proposed boosters for this competition, all of which were indicated as viable: Aerojet and Teledyne Brown proposed three booster engines each with dual combustion chambers, Alliant Techsystems proposed a modified solid rocket booster with lighter casing, more energetic propellant, and four segments instead of five, and Pratt & Whitney Rocketdyne and Dynetics proposed a liquid-fueled booster named Pyrios. However, this competition was planned for a development plan in which Block 1A would be followed by Block 2A, with upgraded boosters. NASA canceled Block 1A and the planned competition in April 2014, in favor of simply remaining with the Ares I's five-segment solid rocket boosters, themselves modified from the Space Shuttle's solid rocket boosters, until at least the late 2020s. The overly powerful advanced booster would have resulted in unsuitably high acceleration, and would need modifications to LC-39B, its flame trench, and Mobile Launcher.

On 31 July 2013, the SLS passed Preliminary Design Review. The review included not only the rocket and boosters but also ground support and logistical arrangements.

On 7 August 2014, the SLS Block 1 passed a milestone known as Key Decision Point C and entered full-scale development, with an estimated launch date of November 2018.

In 2013, NASA and Boeing analyzed the performance of several EUS engine options. The analysis was based on a second-stage usable propellant load of 105 metric tons, and compared stages with four RL10 engines, two MARC-60 engines, or one J-2X engine. In 2014, NASA also considered using the European Vinci instead of the RL10, which offered the same specific impulse but with 64% greater thrust, which would allow for the same performance at a lower cost.

In 2018, Blue Origin submitted a proposal to replace the Exploration Upper Stage with a cheaper alternative to be designed and fabricated by the company, but it was rejected by NASA in November 2019 on multiple grounds; these included lower performance compared to the existing EUS design, incompatibility of the proposal with the height of the door of the Vehicle Assembly Building being only 390 feet (120 m), and unacceptable acceleration of Orion components such as its solar panels.

From 2009 to 2011, three full-duration static fire tests of five-segment solid rocket boosters were conducted under the Constellation Program, including tests at low and high core temperatures, to validate performance at extreme temperatures. The 5-segment solid rocket booster would be carried over to SLS. Northrop Grumman Innovation Systems has completed full-duration static fire tests of the five-segment solid rocket boosters. Qualification Motor 1 was tested on 10 March 2015. Qualification Motor 2 was successfully tested on 28 June 2016.

Operation

Construction

As of 2020, three SLS versions are planned: Block 1, Block 1B, and Block 2. Each will use the same Core stage with its four main engines, but Block 1B will feature the Exploration Upper Stage (EUS), and Block 2 will combine the EUS with upgraded boosters.

The ICPS for Artemis 1 was delivered by ULA to NASA about July 2017 and was housed at Kennedy Space Centre as of November 2018.

In mid-November 2014, construction of the first Core Stage hardware began using a new welding system in the South Vertical Assembly Building at NASA's Michoud Assembly Facility. Between 2015 and 2017, NASA test fired RS-25 engines in preparation for use on SLS.

The core stage for the first SLS, built at Michoud Assembly Facility by Boeing, had all four engines attached in November 2019, and it was declared finished by NASA in December 2019.

The first core stage left Michoud Assembly Facility for comprehensive testing at Stennis Space Center in January 2020. The static firing test program at Stennis Space Center, known as the Green Run, operated all the core stage systems simultaneously for the first time. Test 7 (of 8), the wet dress rehearsal, was carried out in December 2020 and the fire (test 8) took place on 16 January 2021, but shut down earlier than expected, about 67 seconds in total rather than the desired eight minutes. The reason for the early shutdown was later reported to be because of conservative test commit criteria on the thrust vector control system, specific only for ground testing and not for flight. If this scenario occurred during a flight, the rocket would have continued to fly normally. There was no sign of damage to the core stage or the engines, contrary to initial concerns. The second fire test was completed on 18 March 2021, with all 4 engines igniting, throttling down as expected to simulate in-flight conditions, and gimballing profiles. The core stage was shipped to Kennedy Space Center to be mated with the rest of the rocket for Artemis 1. It left Stennis on April 24 and arrived at Kennedy on April 27. It was refurbished there in preparation for stacking. On 12 June 2021, NASA announced the assembly of the first SLS rocket was completed at the Kennedy Space Center. The assembled SLS is planned to be used for the uncrewed Artemis 1 mission in 2022.

While the first SLS for Artemis 1 is being prepared for launch on a test flight in fall 2022, NASA and Boeing are constructing the next three, for Artemis 2, Artemis 3, and Artemis 4. Boeing stated in July 2021 that while the COVID-19 pandemic had affected their suppliers and schedules, such as delaying parts needed for hydraulics, they would still be able to provide the Artemis 2 SLS Core stage per NASA's schedule, with months to spare. The spray-on foam insulation process for Artemis 2 has been automated for most sections of the core stage, saving 12 days in the schedule. The Artemis 2 forward skirt, which is the foremost component of the core stage, was affixed on the liquid oxygen tank in late May 2021. As of July 2022, the complete core stage is set to ship to NASA in March 2023. For Artemis 3, assembly of elements of the thrust structure began at Michoud Assembly Facility in early 2021. The liquid hydrogen tank that is to be used on Artemis 3 was originally planned to be the Artemis 1 tank, but it was set aside as the welds were found to be faulty. Repair techniques were developed, and the tank has reentered production and will be proof tested for strength, for use on Artemis 3.

As of July 2021, Boeing is also preparing to begin construction of the Exploration Upper Stage (EUS), which is planned to debut on Artemis 4.

Planned launches

Originally planned for late 2016, the uncrewed first flight of SLS has slipped more than sixteen times and almost six years. As of earlier that month, the first launch was originally scheduled for 8:30 am EDT, 29 August 2022. It was postponed to 2:17 pm EDT (18:17 UTC), 3 September 2022, after the launch director called a scrub due to a temperature sensor falsely indicating that an RS-25 engine's hydrogen bleed intake was too warm. The 3 September attempt was then scrubbed due to a hydrogen leak in the tail service mast quick disconnect arm, which was fixed; the next launch option was at first a period in late October, due to unfavorable weather during Hurricane Ian. NASA has targeted a launch window between 14 and 27 November 2022, as of October 2022.

NASA limits the amount of time the solid rocket boosters can remain stacked to "about a year" from the time two segments are joined. The first and second segments of the Artemis 1 boosters were joined on 7 January 2021. NASA can choose to extend the time limit based on an engineering review. On 29 September 2021, Northrop Grumman indicated that the limit can be extended to eighteen months for Artemis 1, based on an analysis of the data collected when the boosters were being stacked. In late 2015, the SLS program was stated to have a 70% confidence level for the first Orion flight that carries crew, the second SLS flight overall, by 2023; as of November 2021, NASA delayed Artemis 2 from 2023 to May 2024.

Although the SLS is only confirmed for use on the first few Artemis missions, many NASA mission concept studies for robotic missions planned to launch on the SLS, such as: Neptune Odyssey, Europa Lander, Enceladus Orbilander, Persephone, HabEx, Origins Space Telescope, LUVOIR, Lynx, and Interstellar probe. These concept studies were prepared for possible recommendation by the National Academy's Decadal surveys. The Astronomy and Astrophysics Decadal Survey in 2021 recommended a smaller, merged version of HabEx and LUVOIR preceded by a technology maturation program to reduce cost and schedule risk, although the eventual mission may or may not use SLS. In 2022 the Planetary Science Decadal Survey recommended Enceladus Orbilander as the third highest priority for flagship planetary missions in the 2020s. The Heliophysics Decadal Survey, due to be completed in 2024, is considering the Interstellar Probe mission concept.

Criticism

The SLS has been criticized based on program cost, lack of commercial involvement, and the non-competitive nature of a vehicle legislated to use Space Shuttle components.

Funding

In 2011, Rep. Tom McClintock and other groups called on the Government Accountability Office to investigate possible violations of the Competition in Contracting Act, arguing that Congressional mandates forcing NASA to use Space Shuttle components for the SLS are de facto non-competitive, single-source requirements assuring contracts to existing Shuttle suppliers. The Competitive Space Task Force, in September 2011, said that the new government launcher directly violates NASA's charter, the Space Act, and the 1998 Commercial Space Act requirements for NASA to pursue the "fullest possible engagement of commercial providers" and to "seek and encourage, to the maximum extent possible, the fullest commercial use of space". Opponents of the heavy launch vehicle have critically used the name "Senate launch system", a name that was still being used by opponents to criticize the program in 2021, as "the NASA Inspector General said the total cost of the rocket would reach $27 billion through 2025".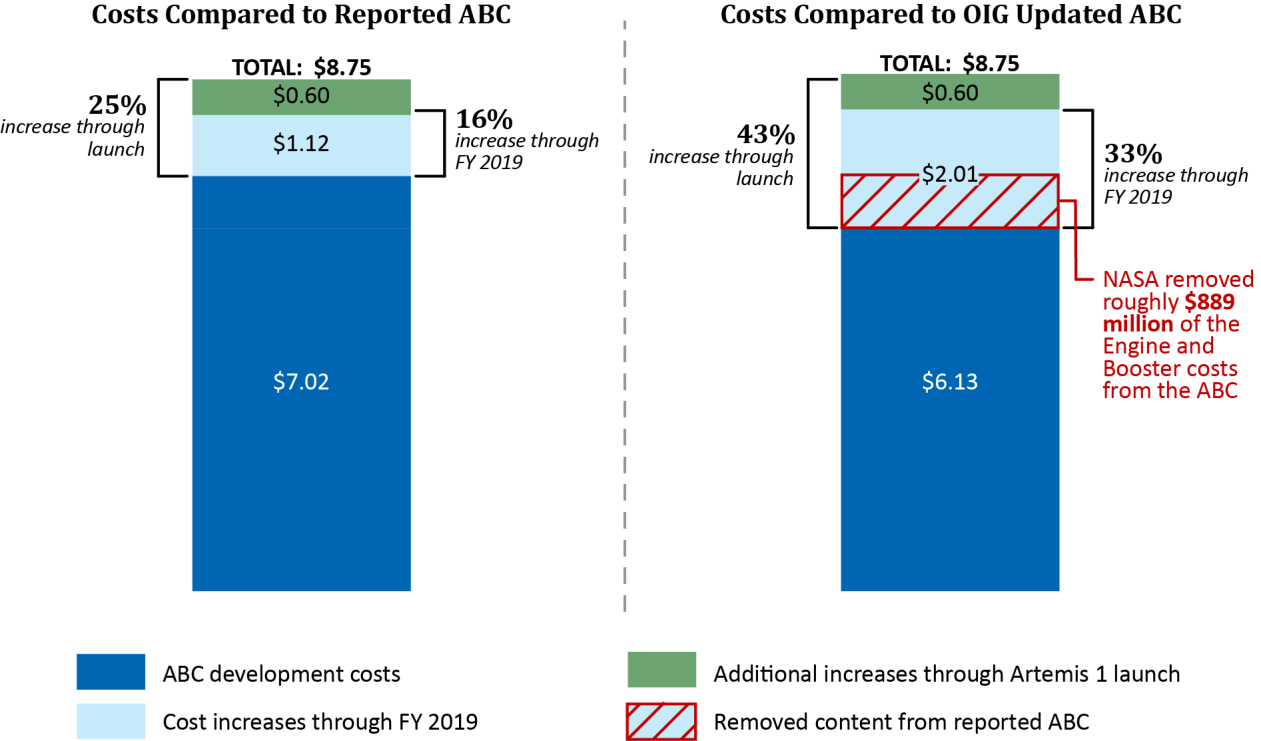

Lori Garver, a former NASA Deputy Administrator, called for canceling the launch vehicle alongside the Mars 2020 rover. Phil Plait shared his criticism of the SLS in light of ongoing budget tradeoffs between the Commercial Crew Development and SLS budgets, also referring to earlier critiques by Garver. In 2019, the Government Accountability Office found that NASA had awarded Boeing over $200 million for service with ratings of good to excellent despite cost overruns and delays. As of 2019, the maiden launch of the SLS was expected in 2021. NASA continued to expect that the first orbital launch would be in 2021 as late as May 2021.

NASA moved out $889 million of costs relating to SLS boosters, but did not update the SLS budget to match, a March 2020 Inspector General report found. This kept the budget overrun to 15% by FY 2019. At 30%, NASA would have to notify Congress and stop funding unless Congress reapproves and provides additional funding. The Inspector General report found that were it not for this "masking" of cost, the overrun would have been 33% by FY 2019. The GAO separately stated "NASA's current approach for reporting cost growth misrepresents the cost performance of the program".

On 1 May 2020, NASA awarded a contract extension to Aerojet Rocketdyne to manufacture 18 additional RS-25 engines with associated services for $1.79 billion, bringing the total RS-25 contract value to almost $3.5 billion. Ars Technica commented that the average cost of each RS-25 therefore rose to $146 million, so each SLS launch uses $580 million for its four engines. Ars noted that for the cost of just one engine, six more powerful RD-180 engines could be purchased, or nearly an entire Falcon Heavy launch with two-thirds of the SLS lift capacity. Former NASA Administrator Charlie Bolden, who oversaw the initial design and development of the SLS, also criticized the program in an interview with Politico in September 2020. Bolden said that the "SLS will go away ... because at some point commercial entities are going to catch up." Bolden further stated, "They are really going to build a heavy-lift launch vehicle sort of like SLS that they will be able to fly for a much cheaper price than NASA can do SLS. That's just the way it works."

Proposed alternatives

In 2009, the Augustine commission proposed a commercial 165,000 lb (75 t) launcher with lower operating costs and noted that a 40–60 t (44–66-short-ton) launcher was the minimum required to support lunar exploration. In 2011–2012, the Space Access Society, Space Frontier Foundation, and The Planetary Society called for the cancellation of the project, arguing that the SLS will consume the funds for other projects from the NASA budget. U.S. Representative Dana Rohrabacher and others proposed that an orbital propellant depot should be developed and the Commercial Crew Development program accelerated instead.

A NASA study that was not publicly released and another from the Georgia Institute of Technology showed this option to be possibly cheaper. In 2012, the United Launch Alliance also suggested using existing rockets with on-orbit assembly and propellant depots as needed. The lack of competition in the SLS design was highlighted. In the summer of 2019, a former ULA employee claimed that Boeing, NASA's prime contractor for SLS, viewed orbital refueling technology as a threat to the SLS and blocked further investment in it. In 2011, Robert Zubrin, founder of Mars Society and Mars Direct, suggested that a heavy lift vehicle could be developed for $5 billion on fixed-price requests for proposal. In 2010, SpaceX's CEO Elon Musk claimed that his company could build a launch vehicle in the 310,000–330,000 lb (140–150 t) payload range for $2.5 billion, or $300 million (in 2010 dollars) per launch, not including a potential upper-stage upgrade.