By Wikipedia,
the free encyclopedia,

https://en.wikipedia.org/wiki/Bi-elliptic_transfer

In astronautics and aerospace engineering, the bi-elliptic transfer is an orbital maneuver that moves a spacecraft from one orbit to another and may, in certain situations, require less delta-v than a Hohmann transfer maneuver.

The bi-elliptic transfer consists of two half-elliptic orbits. From the initial orbit, a first burn expends delta-v to boost the spacecraft into the first transfer orbit with an apoapsis at some point away from the central body. At this point a second burn sends the spacecraft into the second elliptical orbit with periapsis at the radius of the final desired orbit, where a third burn is performed, injecting the spacecraft into the desired orbit.

While they require one more engine burn than a Hohmann transfer and generally requires a greater travel time, some bi-elliptic transfers require a lower amount of total delta-v than a Hohmann transfer when the ratio of final to initial semi-major axis is 11.94 or greater, depending on the intermediate semi-major axis chosen.

The idea of the bi-elliptical transfer trajectory was first published by Ary Sternfeld in 1934.

Calculation

Delta-v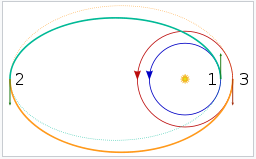

A bi-elliptic transfer from a low circular starting orbit (dark blue) to a higher circular orbit (red)

The three required changes in velocity can be obtained directly from the vis-viva equation

where

• is the speed of an orbiting body,
• is the standard gravitational parameter of the primary body,
• r is the distance of the orbiting body from the primary, i.e., the radius,
• a is the semi-major axis of the body’s orbit.

In what follows,

• r₁ is the radius of the initial circular orbit,
• r₂ is the radius of the final circular orbit,
• r_b is the common apoapsis radius of the two transfer ellipses and is a free parameter of the maneuver,
• a₁ and a₂ are the semimajor axes of the two elliptical transfer orbits, which are given by

  
  

Starting from the initial circular orbit with radius r₁ (dark blue circle in the figure to the right), a prograde burn (mark 1 in the figure) puts the spacecraft on the first elliptical transfer orbit (aqua half-ellipse). The magnitude of the required delta-v for this burn is

When the apoapsis of the first transfer ellipse is reached at a distance r_b from the primary, a second prograde burn (mark 2) raises the periapsis to match the radius of the target circular orbit, putting the spacecraft on a second elliptic trajectory (orange half-ellipse). The magnitude of the required delta-v for the second burn is

Lastly, when the final circular orbit with radius r₂ is reached, a retrograde burn (mark 3) circularizes the trajectory into the final target orbit (red circle). The final retrograde burn requires a delta-v of magnitude

If r_b = r₂, then the maneuver reduces to a Hohmann transfer (in that case can be verified to become zero). Thus the bi-elliptic transfer constitutes a more general class of orbital transfers, of which the Hohmann transfer is a special two-impulse case.

A bi-parabolic transfer from a low circular starting orbit (dark blue) to a higher circular orbit (red)

The maximal possible savings can be computed by assuming that r_b = ∞, in which case the total simplifies to . In this case, one also speaks of a bi-parabolic transfer because the two transfer trajectories are no longer ellipses but parabolas. The transfer time increases to infinity too.

Transfer time

Like the Hohmann transfer, both transfer orbits used in the bi-elliptic transfer constitute exactly one half of an elliptic orbit. This means that the time required to execute each phase of the transfer is half the orbital period of each transfer ellipse.

Using the equation for the orbital period and the notation from above,

The total transfer time t is the sum of the times required for each half-orbit. Therefore:

and finally:

Comparison with the Hohmann transfer

Delta-v

Delta-v required for Hohmann (thick black curve) and bi-elliptic transfers (colored curves) between two circular orbits as a function of the ratio of their radii

The figure shows the total required to transfer from a circular orbit of radius r₁ to another circular orbit of radius r₂. The is shown normalized to the orbital speed in the initial orbit, , and is plotted as a function of the ratio of the radii of the final and initial orbits, ; this is done so that the comparison is general (i.e. not dependent of the specific values of r₁ and r₂, only on their ratio).

The thick black curve indicates the for the Hohmann transfer, while the thinner colored curves correspond to bi-elliptic transfers with varying values of the parameter , defined as the apoapsis radius r_b of the elliptic auxiliary orbit normalized to the radius of the initial orbit, and indicated next to the curves. The inset shows a close-up of the region where the bi-elliptic curves cross the Hohmann curve for the first time.

One sees that the Hohmann transfer is always more efficient if the ratio of radii R is smaller than 11.94. On the other hand, if the radius of the final orbit is more than 15.58 times larger than the radius of the initial orbit, then any bi-elliptic transfer, regardless of its apoapsis radius (as long as it’s larger than the radius of the final orbit), requires less than a Hohmann transfer. Between the ratios of 11.94 and 15.58, which transfer is best depends on the apoapsis distance r_b. For any given R in this range, there is a value of r_b above which the bi-elliptic transfer is superior and below which the Hohmann transfer is better. The following table lists the value of that results in the bi-elliptic transfer being better for some selected cases.

Minimal such that a bi-elliptic transfer needs less

Ratio of radii, {\displaystyle	Minimal {\displaystyle \alpha \equiv	Comments
<11.94	N/A	Hohmann transfer is always better
11.94	∞	Bi-parabolic transfer
12	815.81
13	48.90
14	26.10
15	18.19
15.58	15.58
>15.58		Any bi-elliptic transfer is better

Transfer time

The long transfer time of the bi-elliptic transfer,

is a major drawback for this maneuver. It even becomes infinite for the bi-parabolic transfer limiting case.

The Hohmann transfer takes less than half of the time because there is just one transfer half-ellipse, to be precise,

Example

To transfer from a circular low Earth orbit with r₀ = 6700 km to a new circular orbit with r₁ = 93 800 km using a Hohmann transfer orbit requires a Δv of 2825.02 + 1308.70 = 4133.72 m/s. However, because r₁ = 14r₀ > 11.94r₀, it is possible to do better with a bi-elliptic transfer. If the spaceship first accelerated 3061.04 m/s, thus achieving an elliptic orbit with apogee at r₂ = 40r₀ = 268 000 km, then at apogee accelerated another 608.825 m/s to a new orbit with perigee at r₁ = 93 800 km, and finally at perigee of this second transfer orbit decelerated by 447.662 m/s, entering the final circular orbit, then the total Δv would be only 4117.53 m/s, which is 16.19 m/s (0.4%) less.

The Δv saving could be further improved by increasing the intermediate apogee, at the expense of longer transfer time. For example, an apogee of 75.8r₀ = 507 688 km (1.3 times the distance to the Moon) would result in a 1% Δv saving over a Hohmann transfer, but require a transit time of 17 days. As an impractical extreme example, an apogee of 1757r₀ = 11 770 000 km (30 times the distance to the Moon) would result in a 2% Δv saving over a Hohmann transfer, but the transfer would require 4.5 years (and, in practice, be perturbed by the gravitational effects of other Solar system bodies). For comparison, the Hohmann transfer requires 15 hours and 34 minutes.

Evidently, the bi-elliptic orbit spends more of its delta-v early on (in the first burn). This yields a higher contribution to the specific orbital energy and, due to the Oberth effect, is responsible for the net reduction in required delta-v.

Text from Wikipedia is available under the Creative Commons Attribution/Share-Alike License; additional terms may apply.

Published in April 2019.

Click here to read more articles related to aviation and space!