Angular velocity

In physics, angular velocity refers to how fast an object rotates or revolves relative to another point, i.e. how fast the angular position or orientation of an object changes with time. There are two types of angular velocity: orbital angular velocity and spin angular velocity. Spin angular velocity refers to how fast a rigid body rotates with respect to its centre of rotation. Orbital angular velocity refers to how fast a rigid body’s centre of rotation revolves about a fixed origin, i.e. the time rate of change of its angular position relative to the origin. In general, angular velocity is measured in angle per unit time, e.g. radians per second. The SI unit of angular velocity is expressed as radians/sec with the radian having a dimensionless value of unity, thus the SI units of angular velocity are listed as 1/sec. Angular velocity is usually represented by the symbol omega (ω, sometimes Ω). By convention, positive angular velocity indicates counter-clockwise rotation, while negative is clockwise.

For example, a geostationary satellite completes one orbit per day above the equator, or 360 degrees per 24 hours, and has angular velocity ω = 360 / 24 = 15 degrees per hour, or 2π / 24 ≈ 0.26 radians per hour. If angle is measured in radians, the linear velocity is the radius times the angular velocity,

With orbital radius 42,000 km from the earth’s center, the satellite’s speed through space is thus v = 42,000 × 0.26 ≈ 11,000 km/hr. The angular velocity is positive since the satellite travels eastward with the Earth’s rotation (counter-clockwise from above the north pole.)

In three dimensions, angular velocity is a pseudovector, with its magnitude measuring the rate at which an object rotates or revolves, and its direction pointing perpendicular to the instantaneous plane of rotation or angular displacement. The orientation of angular velocity is conventionally specified by the right-hand rule.

Orbital angular velocity of a point particle

Particle in two dimensions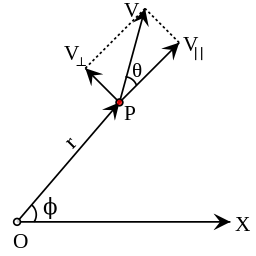

The angular velocity of the particle at Pwith respect to the origin O is determined by the perpendicular component of the velocity vector v.

In the simplest case of circular motion at radius r, with position given by the angular displacement

from the x-axis, the orbital angular velocity is the rate of change of angle with respect to time:

. If

is measured in radians, the distance from the x-axis around the circle to the particle is

, and the linear velocity is

, so that

In the general case of a particle moving in the plane, the orbital angular velocity is the rate at which the position vector relative to a chosen origin «sweeps out» angle. The diagram shows the position vector r from the origin O to a particle P, with its polar coordinates

. (All variables are functions of time t.) The particle has linear velocity splitting as

, with the radial component

parallel to the radius, and the cross-radial (or tangential) component

perpendicular to the radius. When there is no radial component, the particle moves around the origin in a circle; but when there is no cross-radial component, it moves in a straight line from the origin. Since radial motion leaves the angle unchanged, only the cross-radial component of linear velocity contributes to angular velocity.

The angular velocity ω is the rate of change of angular position with respect to time, which can be computed from the cross-radial velocity as:

Here the cross-radial speed

is the signed magnitude of

, positive for counter-clockwise motion, negative for clockwise. Taking polar coordinates for the linear velocity v gives magnitude v (linear speed) and angle θ relative to the radius vector; in these terms,

, so that

These formulas may be derived from

and

, together with the projection formula

, where

In two dimensions, angular velocity is a number with plus or minus sign indicating orientation, but not pointing in a direction. The sign is conventionally taken to be positive if the radius vector turns counter-clockwise, and negative if clockwise. Angular velocity then may be termed a pseudoscalar, a numerical quantity which changes sign under a parity inversion, such as inverting one axis or switching the two axes.

Particle in three dimensions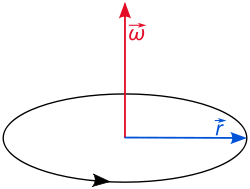

The orbital angular velocity vector encodes the time rate of change of angular position, as well as the instantaneous plane of angular displacement. In this case (counter-clockwise circular motion) the vector points up.

In three-dimensional space, we again have the position vector r of a moving particle. Here, orbital angular velocity is a pseudovector whose magnitude is the rate at which r sweeps out angle, and whose direction is perpendicular to the instantaneous plane in which r sweeps out angle (i.e. the plane spanned by r and v). However, as there are two directions perpendicular to any plane, an additional condition is necessary to uniquely specify the direction of the angular velocity; conventionally, the right-hand rule is used.

Let the pseudovector

u

be the unit vector perpendicular to the plane spanned by r and v, so that the right-hand rule is satisfied (i.e. the instantaneous direction of angular displacement is counter-clockwise looking from the top of

u

). Taking polar coordinates

in this plane, as in the two-dimensional case above, one may define the orbital angular velocity vector as:

Addition of angular velocity vectors

Schematic construction for addition of angular velocity vectors for rotating frames.

If a point rotates with orbital angular velocity ω₁ about its center of rotation in a coordinate frame

F 1 which itself rotates with a spin angular velocity ω 2 with respect to an external frame F 2, we can define ω 1 + ω 2 to be the composite orbital angular velocity vector of the point about its center of rotation with respect to F 2 . This operation coincides with usual addition of vectors, and it gives angular velocity the algebraic structure of a true vector, rather than just a pseudo-vector.

The only non-obvious property of the above addition is commutativity. This can be proven from the fact that the velocity tensor W (see below) is skew-symmetric, so that

is a rotation matrix which can be expanded as

. The composition of rotations is not commutative, but

is commutative to first order, and therefore

ω 1 + ω 2 = ω 2 + ω 1

Notice that this also defines the substraction as the addition of a negative vector.

Spin angular velocity vector for a frame

Given a rotating frame of three unit coordinate vectors, all the three must have the same angular speed at each instant. In such a frame, each vector may be considered as a moving particle with constant scalar radius.

The rotating frame appears in the context of rigid bodies, and special tools have been developed for it: the spin angular velocity may be described as a vector or equivalently as a tensor.

Consistent with the general definition, the spin angular velocity of a frame is defined as the orbital angular velocity of any of the three vectors (same for all) with respect to its own centre of rotation. The addition of angular velocity vectors for frames is also defined by the usual vector addition (composition of linear movements), and can be useful to decompose the rotation as in a gimbal. Components of the vector can be calculated as derivatives of the parameters defining the moving frames (Euler angles or rotation matrices). As in the general case, addition is commutative:

By Euler’s rotation theorem, any rotating frame possesses an instantaneous axis of rotation, which is the direction of the angular velocity vector, and the magnitude of the angular velocity is consistent with the two-dimensional case.

Components from the vectors of the frame

Considering a coordinate vector of the frame as a particle,

we obtain the orbital angular velocity vector:

Components from Euler angles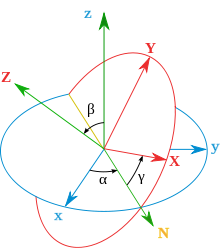

Diagram showing Euler frame in green.

The components of the spin angular velocity pseudovector were first calculated by Leonhard Euler using his Euler angles and the use of an intermediate frame:

Euler proved that the projections of the angular velocity pseudovector on each of these three axes is the derivative of its associated angle (which is equivalent to decomposing the instantaneous rotation into three instantaneous Euler rotations). Therefore:

This basis is not orthonormal and it is difficult to use, but now the velocity vector can be changed to the fixed frame or to the moving frame with just a change of bases. For example, changing to the mobile frame:

where i, j, k are unit vectors for the frame fixed in the moving body. This example has been made using the Z-X-Z convention for Euler angles.

Angular velocity tensor

The angular velocity vector ω=(ω_x,ω_y,ω_z) defined above may be equivalently expressed as an angular velocity tensor, the matrix (or linear mapping) W = W(t) defined by:

Calculation from the orientation matrix

Given the orientation matrix A(t) of a frame, whose columns are the moving orthonormal coordinate vectors

e 1, e 2

,e₃ we can obtain its angular velocity tensor W(t) as follows. Angular velocity must be the same for the three vectors r=

e i

, so arranging the three vector equations into columns of a matrix, we have:

(This holds even if A(t) does not rotate uniformly.) Therefore the angular velocity tensor is:

Properties of angular velocity tensors

This tensor W will have n(n−1)/2 independent components, which is the dimension of the Lie algebra of the Lie group of rotations of an n-dimensional inner product space.

Duality with respect to the velocity vector

In three dimensions, angular velocity can be represented by a pseudovector because second rank tensors are dual to pseudovectors in three dimensions. Since the angular velocity tensor W = W(t) is a skew-symmetric matrix:

its Hodge dual is a vector, which is precisely the previous angular velocity vector ω=[ω_x,ω_y,ω_z].

Exponential of W

If we know an initial frame A(0) and we are given a constant angular velocity tensor W, we can obtain A(t) for any given t. Recall the matrix differential equation:

W is skew-symmetric

A rotation matrix A is orthogonal, inverse to its transpose, so we have

. For

a frame matrix, taking the time derivative of the equation gives:

Coordinate-free description

At any instant

t

, the angular velocity tensor represents a linear map between the position vector

r(t)

and the velocity vectors

v(t)

of a point on a rigid body rotating around the origin:

The relation between this linear map and the angular velocity pseudovector ω is the following.

is skew-symmetric. Thus we can apply the fact of exterior algebra that there is a unique linear form

that

Introducing

, as the Hodge dual of L^♯, and applying the definition of the Hodge dual twice supposing that the preferred unit 3-vector is

*1

Because

s

is an arbitrary vector, from nondegeneracy of scalar product follows

Angular velocity as a vector field

Since the spin angular velocity tensor of a rigid body (in its rest frame) is a linear transformation that maps positions to velocities (within the rigid body), it can be regarded as a constant vector field. In particular, the spin angular velocity is a Killing vector field belonging to an element of the Lie algebra SO(3) of the 3-dimensional rotation group SO(3). Also, it can be shown that the spin angular velocity vector field is exactly half of the curl of the linear velocity vector field v(r) of the rigid body.

Rigid body considerations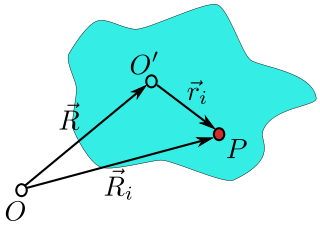

Position of point P located in the rigid body (shown in blue). R_i is the position with respect to the lab frame, centered at O and r_i is the position with respect to the rigid body frame, centered at O′. The origin of the rigid body frame is at vector position R from the lab frame.

The same equations for the angular speed can be obtained reasoning over a rotating rigid body. Here is not assumed that the rigid body rotates around the origin. Instead, it can be supposed rotating around an arbitrary point that is moving with a linear velocity V(t) in each instant.

To obtain the equations, it is convenient to imagine a rigid body attached to the frames and consider a coordinate system that is fixed with respect to the rigid body. Then we will study the coordinate transformations between this coordinate and the fixed «laboratory» system.

As shown in the figure on the right, the lab system’s origin is at point O, the rigid body system origin is at O′and the vector from O to O′ is R. A particle (i) in the rigid body is located at point P and the vector position of this particle is R_i in the lab frame, and at position r_i in the body frame. It is seen that the position of the particle can be written:

The defining characteristic of a rigid body is that the distance between any two points in a rigid body is unchanging in time. This means that the length of the vector r_i is unchanging. By Euler’s rotation theorem, we may replace the vector r_i with

Rr io

where

R

is a 3×3 rotation matrix and r_io is the position of the particle at some fixed point in time, say t = 0. This replacement is useful, because now it is only the rotation matrix

R

that is changing in time and not the reference vector r_io, as the rigid body rotates about point O′. Also, since the three columns of the rotation matrix represent the three versors of a reference frame rotating together with the rigid body, any rotation about any axis becomes now visible, while the vector r_i would not rotate if the rotation axis were parallel to it, and hence it would only describe a rotation about an axis perpendicular to it (i.e., it would not see the component of the angular velocity pseudovector parallel to it, and would only allow the computation of the component perpendicular to it). The position of the particle is now written as:

where V_i is the velocity of the particle (in the lab frame) and V is the velocity of O′ (the origin of the rigid body frame). Since R is a rotation matrix its inverse is its transpose. So we substitute

It can be proved that this is a skew symmetric matrix, so we can take its dual to get a 3 dimensional pseudovector that is precisely the previous angular velocity vector

Substituting ω for W into the above velocity expression, and replacing matrix multiplication by an equivalent cross product:

It can be seen that the velocity of a point in a rigid body can be divided into two terms – the velocity of a reference point fixed in the rigid body plus the cross product term involving the orbital angular velocity of the particle with respect to the reference point. This angular velocity is what physicists call the «spin angular velocity» of the rigid body, as opposed to the orbital angular velocity of the reference point O′ about the origin O.

Consistency

We have supposed that the rigid body rotates around an arbitrary point. We should prove that the spin angular velocity previously defined is independent of the choice of origin, which means that the spin angular velocity is an intrinsic property of the spinning rigid body. (Note the marked contrast of this with the orbital angular velocity of a point particle, which certainly does depend on the choice of origin.)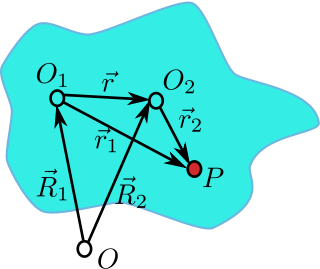

Proving the independence of spin angular velocity from choice of origin.

See the graph to the right: The origin of lab frame is O, while O₁ and O₂ are two fixed points on the rigid body, whose velocity is

v 1

and

v 2

respectively. Suppose the angular velocity with respect to O₁ and O₂ is ω₁ and ω₂ respectively. Since point P and O₂ have only one velocity,

If the reference point is the instantaneous axis of rotation the expression of the velocity of a point in the rigid body will have just the angular velocity term. This is because the velocity of the instantaneous axis of rotation is zero. An example of the instantaneous axis of rotation is the hinge of a door. Another example is the point of contact of a purely rolling spherical (or, more generally, convex) rigid body.