 |
 |
|
||||
|
By
Wikipedia, The Northrop (later Northrop Grumman) B-2 Spirit, also known as the Stealth Bomber, is an American heavy strategic bomber, featuring low observable stealth technology designed for penetrating dense anti-aircraft defenses. Designed during the Cold War, it is a flying wing design with a crew of two. The bomber is subsonic and can deploy both conventional and thermonuclear weapons, such as up to eighty 500-pound class (230 kg) Mk 82 JDAM GPS-guided bombs, or sixteen 2,400-pound (1,100 kg) B83 nuclear bombs. The B-2 is the only acknowledged aircraft that can carry large air-to-surface standoff weapons in a stealth configuration. Northrop Grumman B-2 Spirit
A U.S. Air Force B-2 Spirit flying over the Pacific Ocean in May 2006.
Role: Stealth strategic heavy bomber Development started under the "Advanced Technology Bomber" (ATB) project during the Carter administration; its expected performance was one of the President's reasons for the cancellation of the Mach 2 capable B-1A bomber. The ATB project continued during the Reagan administration, but worries about delays in its introduction led to the reinstatement of the B-1 program. Program costs rose throughout development. Designed and manufactured by Northrop, later Northrop Grumman, the cost of each aircraft averaged US$737 million (in 1997 dollars). Total procurement costs averaged $929 million per aircraft, which includes spare parts, equipment, retrofitting, and software support. The total program cost, which included development, engineering and testing, averaged $2.13 billion per aircraft in 1997. Because of its considerable capital and operating costs, the project was controversial in the U.S. Congress. The winding-down of the Cold War in the latter portion of the 1980s dramatically reduced the need for the aircraft, which was designed with the intention of penetrating Soviet airspace and attacking high-value targets. During the late 1980s and 1990s, Congress slashed plans to purchase 132 bombers to 21. In 2008, a B-2 was destroyed in a crash shortly after takeoff, though the crew ejected safely. As of 2018, twenty B-2s are in service with the United States Air Force, which plans to operate them until 2032, when the Northrop Grumman B-21 Raider is to replace them. The B-2 is capable of all-altitude attack missions up to 50,000 feet (15,000 m), with a range of more than 6,000 nautical miles (6,900 mi; 11,000 km) on internal fuel and over 10,000 nautical miles (12,000 mi; 19,000 km) with one midair refueling. It entered service in 1997 as the second aircraft designed to have advanced stealth technology after the Lockheed F-117 Nighthawk attack aircraft. Though designed originally as primarily a nuclear bomber, the B-2 was first used in combat dropping conventional, non-nuclear ordnance in the Kosovo War in 1999. It later served in Iraq, Afghanistan, and Libya. DevelopmentOriginsBy the mid-1970s, military aircraft designers had learned of a new method to avoid missiles and interceptors, known today as "stealth". The concept was to build an aircraft with an airframe that deflected or absorbed radar signals so that little was reflected back to the radar unit. An aircraft having radar stealth characteristics would be able to fly nearly undetected and could be attacked only by weapons and systems not relying on radar. Although other detection measures existed, such as human observation, infrared scanners, acoustic locators, their relatively short detection range or poorly-developed technology allowed most aircraft to fly undetected, or at least untracked, especially at night. In 1974, DARPA requested information from U.S. aviation firms about the largest radar cross-section of an aircraft that would remain effectively invisible to radars. Initially, Northrop and McDonnell Douglas were selected for further development. Lockheed had experience in this field due to developing the Lockheed A-12 and SR-71, which included a number of stealthy features, notably its canted vertical stabilizers, the use of composite materials in key locations, and the overall surface finish in radar-absorbing paint. A key improvement was the introduction of computer models used to predict the radar reflections from flat surfaces where collected data drove the design of a "faceted" aircraft. Development of the first such designs started in 1975 with "the Hopeless Diamond", a model Lockheed built to test the concept. Plans were well advanced by the summer of 1975, when DARPA started the Experimental Survivability Testbed (XST) project. Northrop and Lockheed were awarded contracts in the first round of testing. Lockheed received the sole award for the second test round in April 1976 leading to the Have Blue program and eventually the F-117 stealth attack aircraft. Northrop also had a classified technology demonstration aircraft, the Tacit Blue in development in 1979 at Area 51. It developed stealth technology, LO (low observables), fly-by-wire, curved surfaces, composite materials, electronic intelligence (ELINT), and Battlefield Surveillance Aircraft Experimental (BSAX). "The stealth technology developed from the program was later incorporated into other operational aircraft designs, including the B-2 stealth bomber". ATB programBy 1976, these programs had progressed to a position in which a long-range strategic stealth bomber appeared viable. President Carter became aware of these developments during 1977, and it appears to have been one of the major reasons the B-1 was canceled. Further studies were ordered in early 1978, by which point the Have Blue platform had flown and proven the concepts. During the 1980 presidential election campaign in 1979, Ronald Reagan repeatedly stated that Carter was weak on defense, and used the B-1 as a prime example. In response, on 22 August 1980 the Carter administration publicly disclosed that the United States Department of Defense was working to develop stealth aircraft, including a bomber. The Advanced Technology Bomber (ATB) program began in 1979. Full development of the black project followed, and was funded under the code name "Aurora". After the evaluations of the companies' proposals, the ATB competition was narrowed to the Northrop/Boeing and Lockheed/Rockwell teams with each receiving a study contract for further work. Both teams used flying wing designs. The Northrop proposal was code named "Senior Ice" and the Lockheed proposal code named "Senior Peg". Northrop had prior experience developing the YB-35 and YB-49 flying wing aircraft. The Northrop design was larger while the Lockheed design included a small tail. In 1979, designer Hal Markarian produced a sketch of the aircraft, that bore considerable similarities to the final design. The USAF originally planned to procure 165 of the ATB bomber. 
The B-2's first public display in 1988 at Palmdale, California: in front of the B-2 is a star shape formed with five B-2 silhouettes. The Northrop team's ATB design was selected over the Lockheed/Rockwell design on 20 October 1981. The Northrop design received the designation B-2 and the name "Spirit". The bomber's design was changed in the mid-1980s when the mission profile was changed from high-altitude to low-altitude, terrain-following. The redesign delayed the B-2's first flight by two years and added about US$1 billion to the program's cost. An estimated US$23 billion was secretly spent for research and development on the B-2 by 1989. MIT engineers and scientists helped assess the mission effectiveness of the aircraft under a five-year classified contract during the 1980s. Secrecy and espionageDuring its design and development, the Northrop B-2 program was a "black" project requiring a secret clearance for all program personnel before its revelation to the public. Unlike the Lockheed F-117 program, which was also a black project (the type of military project which very few people knew even existed while it was being designed and developed), more people within the United States federal government knew about the B-2 and more information about the project was available. Both during development and in service, considerable effort has been devoted to maintaining the security of the B-2's design and technologies. Staff working on the B-2 in most, if not all, capacities have to achieve a level of special-access clearance, and undergo extensive background checks carried out by a special branch of the USAF. For the manufacturing, a former Ford automobile assembly plant in Pico Rivera, California, was acquired and heavily rebuilt; the plant's employees were sworn to complete secrecy regarding their work. To avoid the possibility of suspicion, components were typically purchased through front companies, military officials would visit out of uniform, and staff members were routinely subjected to polygraph examinations. The secrecy extended so far that access to nearly all information on the program by both Government Accountability Office (GAO) and virtually all members of Congress itself was severely limited until the mid-1980s. Northrop (now Northrop Grumman) was the B-2's prime contractor; major subcontractors included Boeing, Hughes Aircraft (now Raytheon), GE, and Vought Aircraft. In 1984, a Northrop employee, Thomas Cavanaugh, was arrested for attempting to sell classified information to the Soviet Union; the information was taken from Northrop's Pico Rivera, California factory. Cavanaugh was eventually sentenced to life in prison and released on parole in 2001. The B-2 was first publicly displayed on 22 November 1988 at United States Air Force Plant 42 in Palmdale, California, where it was assembled. This viewing was heavily restricted, and guests were not allowed to see the rear of the B-2. However, Aviation Week editors found that there were no airspace restrictions above the presentation area and took aerial photographs of the aircraft's then-secret rear section with suppressed engine exhausts. The B-2's (s/n 82-1066 / AV-1) first public flight was on 17 July 1989 from Palmdale to Edwards AFB. In October 2005, Noshir Gowadia, a design engineer who worked on the B-2's propulsion system, was arrested for selling B-2 related classified information to China. Gowadia was convicted and sentenced to 32 years in prison for his actions. Program costs and procurementA procurement of 132 aircraft was planned in the mid-1980s, but was later reduced to 75. By the early 1990s the Soviet Union dissolved, effectively eliminating the Spirit's primary Cold War mission. Under budgetary pressures and Congressional opposition, in his 1992 State of the Union Address, President George H. W. Bush announced B-2 production would be limited to 20 aircraft. In 1996, however, the Clinton administration, though originally committed to ending production of the bombers at 20 aircraft, authorized the conversion of a 21st bomber, a prototype test model, to Block 30 fully operational status at a cost of nearly $500 million. In 1995, Northrop made a proposal to the USAF to build 20 additional aircraft with a flyaway cost of $566 million each. The program was the subject of public controversy for its cost to American taxpayers. In 1996, the General Accounting Office (GAO) disclosed that the USAF's B-2 bombers "will be, by far, the most costly bombers to operate on a per aircraft basis", costing over three times as much as the B-1B (US$9.6 million annually) and over four times as much as the B-52H (US$6.8 million annually). In September 1997, each hour of B-2 flight necessitated 119 hours of maintenance in turn. Comparable maintenance needs for the B-52 and the B-1B are 53 and 60 hours respectively for each hour of flight. A key reason for this cost is the provision of air-conditioned hangars large enough for the bomber's 172 ft (52 m) wingspan, which are needed to maintain the aircraft's stealth properties, particularly its "low-observable" stealth skins. Maintenance costs are about $3.4 million a month for each aircraft. An August 1995 GAO report disclosed that the B-2 had trouble operating in heavy rain, as this rain could damage the aircraft's stealth coating, causing procurement delays until an adequate protective coating could be found. In addition, the B-2's terrain-following/terrain-avoidance radar had difficulty distinguishing rain from other obstacles, rendering the subsystem inoperable during rain. However a subsequent report in October 1996 noted that the USAF had made some progress in resolving the issues with the radar via software fixes and hoped to have these fixes undergoing tests by the spring of 1997. The total "military construction" cost related to the program was projected to be US$553.6 million in 1997 dollars. The cost to procure each B-2 was US$737 million in 1997 dollars (equivalent to US$1126 million in 2021), based only on a fleet cost of US$15.48 billion. The procurement cost per aircraft as detailed in GAO reports, which include spare parts and software support, was $929 million per aircraft in 1997 dollars. The total program cost projected through 2004 was US$44.75 billion in 1997 dollars (equivalent to US$68 billion in 2021). This includes development, procurement, facilities, construction, and spare parts. The total program cost averaged US$2.13 billion per aircraft. The B-2 may cost up to $135,000 per flight hour to operate in 2010, which is about twice that of the B-52 and B-1. OppositionIn its consideration of the fiscal year 1990 defense budget, the House Armed Services Committee trimmed $800 million from the B-2 research and development budget, while at the same time staving off a motion to end the project. Opposition in committee and in Congress was mostly broad and bipartisan, with Congressmen Ron Dellums (D-CA), John Kasich (R-OH), and John G. Rowland (R-CT) authorizing the motion to end the project—as well as others in the Senate, including Jim Exon (D-NE) and John McCain (R-AZ) also opposing the project. Dellums and Kasich, in particular, worked together from 1989 through the early 1990s to limit production to 21 aircraft, and were ultimately successful. The escalating cost of the B-2 program and evidence of flaws in the aircraft's ability to elude detection by radar were among factors that drove opposition to continue the program. At the peak production period specified in 1989, the schedule called for spending US$7 billion to $8 billion per year in 1989 dollars, something Committee Chair Les Aspin (D-WI) said "won't fly financially". In 1990, the Department of Defense accused Northrop of using faulty components in the flight control system; it was also found that redesign work was required to reduce the risk of damage to engine fan blades by bird ingestion. In time, a number of prominent members of Congress began to oppose the program's expansion, including later Democratic presidential nominee John Kerry, who cast votes against the B-2 in 1989, 1991 and 1992 while a U.S. Senator, representing Massachusetts. By 1992, Republican President George H. W. Bush called for the cancellation of the B-2 and promised to cut military spending by 30% in the wake of the collapse of the Soviet Union. In October 1995, former Chief of Staff of the United States Air Force, General Mike Ryan, and former Chairman of the Joint Chiefs of Staff, General John Shalikashvili, strongly recommended against Congressional action to fund the purchase of any additional B-2s, arguing that to do so would require unacceptable cuts in existing conventional and nuclear-capable aircraft, and that the military had greater priorities in spending a limited budget. Some B-2 advocates argued that procuring twenty additional aircraft would save money because B-2s would be able to deeply penetrate anti-aircraft defenses and use low-cost, short-range attack weapons rather than expensive standoff weapons. However, in 1995, the Congressional Budget Office (CBO), and its Director of National Security Analysis, found that additional B-2s would reduce the cost of expended munitions by less than US$2 billion in 1995 dollars during the first two weeks of a conflict, in which the USAF predicted bombers would make their greatest contribution; a small fraction of the US$26.8 billion (in 1995 dollars) life cycle cost that the CBO projected for an additional 20 B-2s. In 1997, as Ranking Member of the House Armed Services Committee and National Security Committee, Congressman Ron Dellums (D-CA), a long-time opponent of the bomber, cited five independent studies and offered an amendment to that year's defense authorization bill to cap production of the bombers to the existing 21 aircraft; the amendment was narrowly defeated. Nonetheless, Congress did not approve funding for additional B-2s. Further developmentsA number of upgrade packages have been applied to the B-2. In July 2008, the B-2's onboard computing architecture was extensively redesigned; it now incorporates a new integrated processing unit (IPU) that communicates with systems throughout the aircraft via a newly installed fiber optic network; a new version of the operational flight program software was also developed, with legacy code converted from the JOVIAL programming language to standard C. Updates were also made to the weapon control systems to enable strikes upon moving targets, such as ground vehicles. On 29 December 2008, USAF officials awarded a US$468 million contract to Northrop Grumman to modernize the B-2 fleet's radars. Changing the radar's frequency was required as the United States Department of Commerce had sold that radio spectrum to another operator. In July 2009, it was reported that the B-2 had successfully passed a major USAF audit. In 2010, it was made public that the Air Force Research Laboratory had developed a new material to be used on the part of the wing trailing edge subject to engine exhaust, replacing existing material that quickly degraded. In July 2010, political analyst Rebecca Grant speculated that when the B-2 becomes unable to reliably penetrate enemy defenses, the Lockheed Martin F-35 Lightning II may take on its strike/interdiction mission, carrying B61 nuclear bombs as a tactical bomber. However, in March 2012, the Pentagon announced that a $2 billion, 10-year-long modernization of the B-2 fleet was to begin. The main area of improvement would be replacement of outdated avionics and equipment. Continued modernization efforts likely have continued in secret, as alluded to by a B-2 commander from Whiteman AFB in April 2021, possibly indicating offensive weapons capability against threatening air defenses and aircraft. He stated: without getting into specifics, and without getting into things that we frankly just don't discuss in open channels, I will tell you that our current bomber fleet, and this is all of them, we use some pretty innovative ways to integrate modern weapons capabilities to have us both maintain and increase our survivability. And for the B-2 specifically, the expansion of some of our strike capabilities allow us to increase our survivability beyond the fighter escort realm. Now the B-2 fleet is continuing to do that technological advancement, and that's enabled us to expand our strike capabilities, as well. Although we've been around for over 30 years there's a lot of life left in this platform and up until the B-21 as well on the scene and doing its job, this aircraft will continue to be at the forefront of our country and our nation's defense... and with these, and continued innovative upgrades, and weapons system capabilities we will continue to do that until the last jet flies off the ramp into retirement. It was reported in 2011 that the Pentagon was evaluating an unmanned stealth bomber, characterized as a "mini-B-2", as a potential replacement in the near future. In 2012, USAF Chief of Staff General Norton Schwartz stated the B-2's 1980s-era stealth technologies would make it less survivable in future contested airspaces, so the USAF is to proceed with the Next-Generation Bomber despite overall budget cuts. In 2012 projections, it was estimated that the Next-Generation Bomber would have an overall cost of $55 billion. In 2013, the USAF contracted for the Defensive Management System Modernization program to replace the antenna system and other electronics to increase the B-2's frequency awareness. The Common Very Low Frequency Receiver upgrade will allow the B-2s to use the same very low frequency transmissions as the Ohio-class submarines so as to continue in the nuclear mission until the Mobile User Objective System is fielded. In 2014, the USAF outlined a series of upgrades including nuclear warfighting, a new integrated processing unit, the ability to carry cruise missiles, and threat warning improvements. In 1998, a Congressional panel advised the USAF to refocus resources away from continued B-2 production and instead begin development of a new bomber, either a new build or a variant of the B-2. In its 1999 bomber roadmap the USAF eschewed the panel's recommendations, believing its current bomber fleet could be maintained until the 2030s. The service believed that development could begin in 2013, in time to replace aging B-2s, B-1s and B-52s around 2037. Although the USAF previously planned to operate the B-2 to 2058, the FY 2019 budget moved up its retirement to "no later than 2032". It also moved retirement of the B-1 to 2036 while extending the B-52's service life into the 2050s, due to the latter's lower maintenance costs, versatile conventional payload, and ability to carry nuclear cruise missiles (which the B-1 is treaty-prohibited from doing). The decision to retire the B-2 early was made because the small fleet of 20 is considered too expensive per plane to retain, with its position as a stealth bomber being taken over with the introduction of the B-21 Raider starting in the mid-2020s. DesignOverviewThe B-2 Spirit was developed to take over the USAF's vital penetration missions, able to travel deep into enemy territory to deploy ordnance which could include nuclear weapons. The B-2 is a flying wing aircraft, meaning that it has no fuselage or tail. It has significant advantages over previous bombers due to its blend of low-observable technologies with high aerodynamic efficiency and large payload. Low observability provides a greater freedom of action at high altitudes, thus increasing both range and field of view for onboard sensors. The USAF reports its range as approximately 6,000 nautical miles (6,900 mi; 11,000 km). At cruising altitude, the B-2 refuels every six hours, taking on up to 50 short tons (45,000 kg) of fuel at a time. The development and construction of the B-2 required pioneering use of computer-aided design and manufacturing technologies, due to its complex flight characteristics and design requirements to maintain very low visibility to multiple means of detection. The B-2 bears a resemblance to earlier Northrop aircraft; the YB-35 and YB-49 were both flying wing bombers that had been canceled in development in the early 1950s, allegedly for political reasons. The resemblance goes as far as B-2 and YB-49 having the same wingspan. The YB-49 also had a small radar cross-section. Approximately 80 pilots fly the B-2. Each aircraft has a crew of two, a pilot in the left seat and mission commander in the right, and has provisions for a third crew member if needed. For comparison, the B-1B has a crew of four and the B-52 has a crew of five. The B-2 is highly automated, and one crew member can sleep in a camp bed, use a toilet, or prepare a hot meal while the other monitors the aircraft, unlike most two-seat aircraft. Extensive sleep cycle and fatigue research was conducted to improve crew performance on long sorties. Advanced training is conducted at the USAF Weapons School. Armaments and equipmentThe B-2, in the envisaged Cold War scenario, was to perform deep-penetrating nuclear strike missions, making use of its stealthy capabilities to avoid detection and interception throughout missions. There are two internal bomb bays in which munitions are stored either on a rotary launcher or two bomb-racks; the carriage of the weapons loadouts internally results in less radar visibility than external mounting of munitions. The B-2 is capable of carrying 40,000 lb (18,000 kg) of ordnance. Nuclear ordnance includes the B61 and B83 nuclear bombs; the AGM-129 ACM cruise missile was also intended for use on the B-2 platform. It was decided, in light of the dissolution of the Soviet Union, to equip the B-2 for conventional precision attacks as well as for the strategic role of nuclear-strike. The B-2 features a sophisticated GPS-Aided Targeting System (GATS) that uses the aircraft's APQ-181 synthetic aperture radar to map out targets prior to deployment of GPS-aided bombs (GAMs), later superseded by the Joint Direct Attack Munition (JDAM). In the B-2's original configuration, up to 16 GAMs or JDAMs could be deployed; an upgrade program in 2004 raised the maximum carriable capacity to 80 JDAMs. The B-2 has various conventional weapons in its arsenal, able to equip Mark 82 and Mark 84 bombs, CBU-87 Combined Effects Munitions, GATOR mines, and the CBU-97 Sensor Fuzed Weapon. In July 2009, Northrop Grumman reported the B-2 was compatible with the equipment necessary to deploy the 30,000 lb (14,000 kg) Massive Ordnance Penetrator (MOP), which is intended to attack reinforced bunkers; up to two MOPs could be equipped in the B-2's bomb bays with one per bay, the B-2 is the only platform compatible with the MOP as of 2012. As of 2011, the AGM-158 JASSM cruise missile is an upcoming standoff munition to be deployed on the B-2 and other platforms. This is to be followed by the Long Range Standoff Weapon which may give the B-2 a standoff nuclear capability for the first time. Avionics and systemsTo make the B-2 more effective than previous bombers, many advanced and modern avionics systems were integrated into its design; these have been modified and improved following a switch to conventional warfare missions. One system is the low probability of intercept AN/APQ-181 multi-mode radar, a fully digital navigation system that is integrated with terrain-following radar and Global Positioning System (GPS) guidance, NAS-26 astro-inertial navigation system (first such system tested on the Northrop SM-62 Snark cruise missile) and a Defensive Management System (DMS) to inform the flight crew of possible threats. The onboard DMS is capable of automatically assessing the detection capabilities of identified threats and indicated targets. The DMS will be upgraded by 2021 to detect radar emissions from air defenses to allow changes to the auto-router's mission planning information while in-flight so it can receive new data quickly to plan a route that minimizes exposure to dangers. For safety and fault-detection purposes, an on-board test system is linked with the majority of avionics on the B-2 to continuously monitor the performance and status of thousands of components and consumables; it also provides post-mission servicing instructions for ground crews. In 2008, many of the 136 standalone distributed computers on board the B-2, including the primary flight management computer, were being replaced by a single integrated system. The avionics are controlled by 13 EMP-resistant MIL-STD-1750A computers, which are interconnected through 26 MIL-STD-1553B-busses; other system elements are connected via optical fiber. In addition to periodic software upgrades and the introduction of new radar-absorbent materials across the fleet, the B-2 has had several major upgrades to its avionics and combat systems. For battlefield communications, both Link-16 and a high frequency satellite link have been installed, compatibility with various new munitions has been undertaken, and the AN/APQ-181 radar's operational frequency was shifted to avoid interference with other operators' equipment. The arrays of the upgraded radar features were entirely replaced to make the AN/APQ-181 into an active electronically scanned array (AESA) radar. Due to the B-2's composite structure, it is required to stay 40 miles (64 km) away from thunderstorms, to avoid static discharge and lightning strikes. Flight controls
Vice President Dick Cheney inside a B-2 cockpit with pilot Capt. Luke Jayne during a visit to Whiteman AFB, 2006. To address the inherent flight instability of a flying wing aircraft, the B-2 uses a complex quadruplex computer-controlled fly-by-wire flight control system that can automatically manipulate flight surfaces and settings without direct pilot inputs to maintain aircraft stability. The flight computer receives information on external conditions such as the aircraft's current air speed and angle of attack via pitot-static sensing plates, as opposed to traditional pitot tubes which would impair the aircraft's stealth capabilities. The flight actuation system incorporates both hydraulic and electrical servoactuated components, and it was designed with a high level of redundancy and fault-diagnostic capabilities. Northrop had investigated several means of applying directional control that would infringe on the aircraft's radar profile as little as possible, eventually settling on a combination of split brake-rudders and differential thrust. Engine thrust became a key element of the B-2's aerodynamic design process early on; thrust not only affects drag and lift but pitching and rolling motions as well. Four pairs of control surfaces are located along the wing's trailing edge; while most surfaces are used throughout the aircraft's flight envelope, the inner elevons are normally only in use at slow speeds, such as landing. To avoid potential contact damage during takeoff and to provide a nose-down pitching attitude, all of the elevons remain drooped during takeoff until a high enough airspeed has been attained. Stealth
The B-2's engines are buried within its wing to conceal the engines' fans and minimize their exhaust signature. The B-2's low-observable, or "stealth", characteristics enable the undetected penetration of sophisticated anti-aircraft defenses and to attack even heavily defended targets. This stealth comes from a combination of reduced acoustic, infrared, visual and radar signatures (multi-spectral camouflage) to evade the various detection systems that could be used to detect and be used to direct attacks against an aircraft. The B-2's stealth enables the reduction of supporting aircraft that are required to provide air cover, Suppression of Enemy Air Defenses and electronic countermeasures, making the bomber a "force multiplier". As of September 2013, there have been no instances of a missile being launched at a B-2. To reduce optical visibility during daylight flights, the B-2 is painted in an anti-reflective paint. The undersides are dark because it flies at high altitudes (50,000 ft (15,000 m)), and at that altitude a dark grey painting blends well into the sky. It is speculated to have an upward-facing light sensor which alerts the pilot to increase or reduce altitude to match the changing illuminance of the sky. The original design had tanks for a contrail-inhibiting chemical, but this was replaced in production aircraft by a contrail sensor that alerts the crew when they should change altitude. The B-2 is vulnerable to visual interception at ranges of 20 nmi (23 mi; 37 km) or less. The B-2 is stored in a $5 million specialised air-conditioned hangar to maintain its stealth coating. Every seven years, this coating is carefully removed by being washed off with crystallised wheat starch so that the B-2's surfaces can be inspected for any dents or scratches. RadarReportedly, the B-2 has a radar cross-section (RCS) of about 0.1 m2 (1.1 sq ft). The bomber does not always fly stealthily; when nearing air defenses pilots "stealth up" the B-2, a maneuver whose details are secret. The aircraft is stealthy, except briefly when the bomb bay opens. The B-2's clean, low-drag flying wing configuration not only provides exceptional range but is also beneficial to reducing its radar profile. The flying wing design most closely resembles a so-called infinite flat plate (as vertical control surfaces dramatically increase RCS), the perfect stealth shape, as it would lack angles to reflect back radar waves (initially, the shape of the Northrop ATB concept was flatter; it gradually increased in volume according to specific military requirements). Without vertical surfaces to reflect radar laterally, side aspect radar cross section is also reduced. Radars operating at a lower frequency band (S or L band) are able to detect and track certain stealth aircraft that have multiple control surfaces, like canards or vertical stabilizers, where the frequency wavelength can exceed a certain threshold and cause a resonant effect. 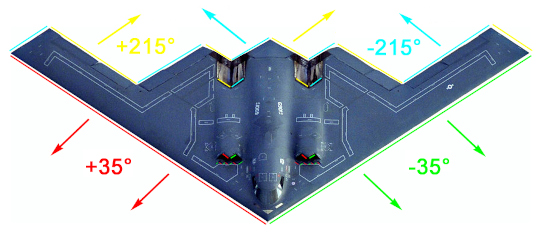
Illustration of the B-2's basic radar reflection angles. RCS reduction as a result of shape had already been observed on the Royal Air Force's Avro Vulcan strategic bomber, and the USAF's F-117 Nighthawk. The F-117 used flat surfaces (faceting technique) for controlling radar returns as during its development (see Lockheed Have Blue) in the early 1970s, technology only allowed for the simulation of radar reflections on simple, flat surfaces; computing advances in the 1980s made it possible to simulate radar returns on more complex curved surfaces. The B-2 is composed of many curved and rounded surfaces across its exposed airframe to deflect radar beams. This technique, known as continuous curvature, was made possible by advances in computational fluid dynamics, and first tested on the Northrop Tacit Blue. InfraredSome analysts claim infra-red search and track systems (IRSTs) can be deployed against stealth aircraft, because any aircraft surface heats up due to air friction and with a two channel IRST is a CO2 (4.3 µm absorption maxima) detection possible, through difference comparing between the low and high channel. 
The gap below the air intake has the purpose of keeping the boundary layer out of the jet engine. Burying engines deep inside the fuselage also minimizes the thermal visibility or infrared signature of the exhaust. At the engine intake, cold air from the boundary layer below the main inlet enters the fuselage (boundary layer suction, first tested on the Northrop X-21) and is mixed with hot exhaust air just before the nozzles (similar to the Ryan AQM-91 Firefly). According to the Stefan–Boltzmann law, this results in less energy (thermal radiation in the infrared spectrum) being released and thus a reduced heat signature. The resulting cooler air is conducted over a surface composed of heat resistant carbon-fiber-reinforced polymer and titanium alloy elements, which disperse the air laterally, to accelerate its cooling. The B-2 lacks afterburners as the hot exhaust would increase the infrared signature; breaking the sound barrier would produce an obvious sonic boom as well as aerodynamic heating of the aircraft skin which would also increase the infrared signature. MaterialsAccording to the Huygens–Fresnel principle, even a very flat plate would still reflect radar waves, though much less than when a signal is bouncing at a right angle. Additional reduction in its radar signature was achieved by the use of various radar-absorbent materials (RAM) to absorb and neutralize radar beams. The majority of the B-2 is made out of a carbon-graphite composite material that is stronger than steel, lighter than aluminum, and absorbs a significant amount of radar energy. The B-2 is assembled with unusually tight engineering tolerances to avoid leaks as they could increase its radar signature. Innovations such as alternate high frequency material (AHFM) and automated material application methods were also incorporated to improve the aircraft's radar-absorbent properties and reduce maintenance requirements. In early 2004, Northrop Grumman began applying a newly developed AHFM to operational B-2s. To protect the operational integrity of its sophisticated radar absorbent material and coatings, each B-2 is kept inside a climate-controlled hangar (Extra Large Deployable Aircraft Hangar System) large enough to accommodate its 172-foot (52 m) wingspan. Shelter systemB-2s are supported by portable, environmentally-controlled hangars called B-2 Shelter Systems (B2SS). The hangars are built by American Spaceframe Fabricators Inc. and cost approximately US$5 million apiece. The need for specialized hangars arose in 1998 when it was found that B-2s passing through Andersen Air Force Base did not have the climate-controlled environment maintenance operations required. In 2003, the B2SS program was managed by the Combat Support System Program Office at Eglin Air Force Base. B2SS hangars are known to have been deployed to Naval Support Facility Diego Garcia and RAF Fairford. Operational history1990s
A B-2 during aerial refueling which extends its range past 6,000 nautical miles (6,900 mi; 11,000 km) for intercontinental sorties. The first operational aircraft, christened Spirit of Missouri, was delivered to Whiteman Air Force Base, Missouri, where the fleet is based, on 17 December 1993. The B-2 reached initial operational capability (IOC) on 1 January 1997. Depot maintenance for the B-2 is accomplished by USAF contractor support and managed at Oklahoma City Air Logistics Center at Tinker Air Force Base. Originally designed to deliver nuclear weapons, modern usage has shifted towards a flexible role with conventional and nuclear capability. The B-2's combat debut was in 1999, during the Kosovo War. It was responsible for destroying 33% of selected Serbian bombing targets in the first eight weeks of U.S. involvement in the War. During this war, six B-2s flew non-stop to Yugoslavia from their home base in Missouri and back, totaling 30 hours. Although the bombers accounted 50 sorties out of a total of 34,000 NATO sorties, they dropped 11 percent of all bombs. The B-2 was the first aircraft to deploy GPS satellite-guided JDAM "smart bombs" in combat use in Kosovo. The use of JDAMs and precision-guided munitions effectively replaced the controversial tactic of carpet-bombing, which had been harshly criticized due to it causing indiscriminate civilian casualties in prior conflicts, such as the 1991 Gulf War. On 7 May 1999, a B-2 dropped five JDAMs on the Chinese Embassy, killing several staff. By then, the B-2 had dropped 500 bombs in Yugoslavia. 2000sThe B-2 saw service in Afghanistan, striking ground targets in support of Operation Enduring Freedom. With aerial refueling support, the B-2 flew one of its longest missions to date from Whiteman Air Force Base in Missouri to Afghanistan and back. B-2s would be stationed in the Middle East as a part of a US military buildup in the region from 2003. The B-2's combat use preceded a USAF declaration of "full operational capability" in December 2003. The Pentagon's Operational Test and Evaluation 2003 Annual Report noted that the B-2's serviceability for Fiscal Year 2003 was still inadequate, mainly due to the maintainability of the B-2's low observable coatings. The evaluation also noted that the Defensive Avionics suite had shortcomings with "pop-up threats". During the Iraq War, B-2s operated from Diego Garcia and an undisclosed "forward operating location". Other sorties in Iraq have launched from Whiteman AFB. As of September 2013 the longest combat mission has been 44.3 hours. "Forward operating locations" have been previously designated as Andersen Air Force Base in Guam and RAF Fairford in the United Kingdom, where new climate controlled hangars have been constructed. B-2s have conducted 27 sorties from Whiteman AFB and 22 sorties from a forward operating location, releasing more than 1,500,000 pounds (680,000 kg) of munitions, including 583 JDAM "smart bombs" in 2003. 2010sIn response to organizational issues and high-profile mistakes made within the USAF, all of the B-2s, along with the nuclear-capable B-52s and the USAF's intercontinental ballistic missiles (ICBMs), were transferred to the newly formed Air Force Global Strike Command on 1 February 2010. In March 2011, B-2s were the first U.S. aircraft into action in Operation Odyssey Dawn, the UN mandated enforcement of the Libyan no-fly zone. Three B-2s dropped 40 bombs on a Libyan airfield in support of the UN no-fly zone. The B-2s flew directly from the U.S. mainland across the Atlantic Ocean to Libya; a B-2 was refueled by allied tanker aircraft four times during each round trip mission. In August 2011, The New Yorker reported that prior to the May 2011 U.S. Special Operations raid into Abbottabad, Pakistan that resulted in the death of Osama bin Laden, U.S. officials had considered an airstrike by one or more B-2s as an alternative; the use of a bunker busting bomb was rejected due to potential damage to nearby civilian buildings. There were also concerns an airstrike would make it difficult to positively identify Bin Laden's remains, making it hard to confirm his death. On 28 March 2013, two B-2s flew a round trip of 13,000 miles (21,000 km) from Whiteman Air Force base in Missouri to South Korea, dropping dummy ordnance on the Jik Do target range. The mission, part of the annual South Korean–United States military exercises, was the first time that B-2s overflew the Korean peninsula. Tensions between the Koreas were high; North Korea protested against the B-2's participation and made threats of retaliatory nuclear strikes against South Korea and the United States. On 18 January 2017, two B-2s attacked an ISIS training camp 19 miles (30 km) southwest of Sirte, Libya, killing around 85 militants. The B-2s together dropped 108 500-pound (230 kg) precision-guided Joint Direct Attack Munition (JDAM) bombs. These strikes were followed by an MQ-9 Reaper unmanned aerial vehicle firing Hellfire missiles. Each B-2 flew a 33-hour, round-trip mission from Whiteman Air Force Base, Missouri with four or five (accounts differ) refuelings during the trip. OperatorsUnited States Air Force (20 aircraft in active inventory)
6520th Flight Test Squadron AccidentsOn 23 February 2008, B-2 "AV-12" Spirit of Kansas crashed on the runway shortly after takeoff from Andersen Air Force Base in Guam. Spirit of Kansas had been operated by the 393rd Bomb Squadron, 509th Bomb Wing, Whiteman Air Force Base, Missouri, and had logged 5,176 flight hours. The two-person crew ejected safely from the aircraft. The aircraft was destroyed, a hull loss valued at US$1.4 billion. After the accident, the USAF took the B-2 fleet off operational status for 53 days, returning on 15 April 2008. The cause of the crash was later determined to be moisture in the aircraft's Port Transducer Units during air data calibration, which distorted the information being sent to the bomber's air data system. As a result, the flight control computers calculated an inaccurate airspeed, and a negative angle of attack, causing the aircraft to pitch upward 30 degrees during takeoff. This was the first crash of a B-2 and the only loss as of 2022. In February 2010, another serious incident involving a B-2 occurred at Andersen Air Force Base. The aircraft involved was AV-11 Spirit of Washington. The aircraft was severely damaged by fire while on the ground and underwent 18 months of repairs to enable it to fly back to the mainland for more comprehensive repairs. Spirit of Washington was repaired and returned to service in December 2013. At the time of the accident the USAF had no training to deal with tailpipe fires on the B-2s. On the night of 13–14 September 2021, a B-2 Spirit of Georgia made an emergency landing at its home base Whiteman AFB. The aircraft landed and went off the runway into the grass and came to rest on its left side. The cause was later determined to be faulty landing gear springs and "microcracking" in hydraulic connections on the aircraft. The lock link springs in the landing gear had likely not been replaced in at least a decade, and produced approximately 11% less tension than specified. This was combined with the disconnection of a hydraulic tube which provides support to the landing gear. Both factors resulted in the gear folding on itself upon landing. The accident resulted in a minimum of $10.1 million in repair damages, but the final repair cost is still being determined. Aircraft on display
Restored B-2 Spirit full-scale test unit on display at the National Museum of the United States Air Force. No operational B-2s have been retired by the Air Force to be put on display. B-2s have made periodic appearances on ground display at various air shows. B-2 test article (s/n AT-1000), the second of two built without engines or instruments for static testing, was placed on display in 2004 at the National Museum of the United States Air Force near Dayton, Ohio. The test article passed all structural testing requirements before the airframe failed. The museum's restoration team spent over a year reassembling the fractured airframe. The display airframe is marked to resemble Spirit of Ohio (S/N 82-1070), the B-2 used to test the design's ability to withstand extreme heat and cold. The exhibit features Spirit of Ohio's nose wheel door, with its Fire and Ice artwork, which was painted and signed by the technicians who performed the temperature testing. The restored test aircraft is on display in the museum's "Cold War Gallery". Specifications (B-2A Block 30)General characteristics
Performance
Armament
Individual aircraft

B-2 in flight over the Mississippi River (St. Louis, Missouri) with the Gateway Arch and Busch Stadium in the background. See also
Text from Wikipedia is available under the Creative Commons Attribution/Share-Alike License; additional terms may apply. Published in October 2022. Click here to read more articles related to aviation and space!
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 |
|
Copyright 2004-2024 © by Airports-Worldwide.com, Vyshenskoho st. 36, Lviv 79010, Ukraine Legal Disclaimer |