Kennedy Space Center Launch Complex 39

Launch Complex 39 (LC-39) is a rocket launch site at the John F. Kennedy Space Center on Merritt Island in Florida, United States. The site and its collection of facilities were originally built as the Apollo program's "Moonport" and later modified for the Space Shuttle program.

Launch Complex 39

LC-39A (foreground) and LC-39B (background) on April 6, 2022.

Location: Kennedy Space Center
Coordinates: 28°36′30.2″N 80°36′15.6″W
Time zone: UTC−05:00 (EST)
• Summer (DST): UTC−04:00 (EDT)
Short name: LC-39
Established: 1962; 60 years ago
Operator:
LC-39A: NASA (1967–2014), SpaceX (2014–present)
LC-39B: NASA (1969–present)
Total launches: 208 (13 Saturn V, 4 Saturn IB, 135 Shuttle, 1 Ares I, 52 Falcon 9, 3 Falcon Heavy)
Launch pad(s): 3
Orbital inclination range: 28°–62°

Launch Complex 39 consists of three launch sub-complexes or "pads"—39A, 39B, and 39C—a Vehicle Assembly Building (VAB), a Crawlerway used by crawler-transporters to carry mobile launcher platforms between the VAB and the pads, Orbiter Processing Facility buildings, a Launch Control Center which contains the firing rooms, a news facility famous for the iconic countdown clock seen in television coverage and photos, and various logistical and operational support buildings.

SpaceX leases Launch Complex 39A from NASA and has modified the pad to support Falcon 9 and Falcon Heavy launches. NASA began modifying Launch Complex 39B in 2007 to accommodate the now defunct Constellation program, and is currently preparing it for the Artemis program, whose first launch is planned for 2022. A pad to be designated 39C, which would have been a copy of pads 39A and 39B, was originally planned for Apollo but never built. A smaller pad, also designated 39C, was constructed from January to June 2015, to accommodate small-lift launch vehicles.

Pad 39A launch history

Status: Active
Launches: 149 (12 Saturn V, 82 Shuttle, 52 Falcon 9, 3 Falcon Heavy)
First launch:

November 9, 1967
Saturn V SA-501

Last launch:

October 5, 2022
Falcon 9 Block 5 / SpaceX Crew-5

Associated rockets:

Saturn V (retired)
Space Shuttle (retired)
Falcon 9 (current)
Falcon Heavy (current)
Starship (future)

Pad 39B launch history

Status: Active
Launches: 59 (1 Saturn V, 4 Saturn IB, 53, Shuttle, 1 Ares I-X) First launch:

May 18, 1969
Saturn V SA-505

Last launch:

October 28, 2009
Ares I-X

Associated rockets:

Saturn IB (retired)
Saturn V (retired)
Space Shuttle (retired)
Ares I-X (retired)
SLS (current)

Pad 39C launch history

Status: Inactive

Launch Complex 39

Location: John F. Kennedy Space Center, Titusville, Florida
Area: 7,000 acres (2,800 ha)
Built: 1967
MPS: John F. Kennedy Space Center MPS
NRHP reference No.: 73000568
Added to NRHP: May 24, 1973

NASA launches from pads 39A and 39B have been supervised from the NASA Launch Control Center (LCC), located 3 miles (4.8 km) from the launch pads. LC-39 is one of several launch sites that share the radar and tracking services of the Eastern Test Range.

History

Early history

Northern Merritt Island was first developed around 1890 when a few wealthy Harvard University graduates purchased 18,000 acres (73 km2) and constructed a three-story mahogany clubhouse, very nearly on the site of Pad 39A. During the 1920s, Peter E. Studebaker Jr., son of the automobile magnate, built a small casino at De Soto Beach eight miles (13 km) north of the Canaveral lighthouse.

In 1948, the Navy transferred the former Banana River Naval Air Station, located south of Cape Canaveral, to the Air Force for use in testing captured German V-2 rockets. The site's location on the East Florida coast was ideal for this purpose, in that launches would be over the ocean, away from populated areas. This site became the Joint Long Range Proving Ground in 1949 and was renamed Patrick Air Force Base in 1950 and Patrick Space Force Base in 2020. The Air Force annexed part of Cape Canaveral, to the north, in 1951, forming the Air Force Missile Test Center, the future Cape Canaveral Space Force Station (CCSFS). Missile and rocketry testing and development would take place here through the 1950s.

After the creation of NASA in 1958, the CCAFS launch pads were used for NASA's civilian uncrewed and crewed launches, including those of Project Mercury and Project Gemini.

Apollo and Skylab

In 1961, President Kennedy proposed to Congress the goal of landing a man on the Moon by the end of the decade. Congressional approval led to the launch of the Apollo program, which required a massive expansion of NASA operations, including an expansion of launch operations from the Cape to adjacent Merritt Island to the north and west. NASA began acquisition of land in 1962, taking title to 131 square miles (340 km2) by outright purchase and negotiating with the state of Florida for an additional 87 square miles (230 km2). On July 1, 1962, the site was named the Launch Operations Center.

The need for a new launch complex was first considered in 1961. At the time, the highest-numbered launch pad at CCAFS was Launch Complex 37. A proposed Launch Complex 38 had been set aside for the future expansion of the Atlas-Centaur program, but ultimately never built. The new complex was thus designated Launch Complex 39.

The method of reaching the Moon had not yet been decided. The two leading alternatives were direct ascent, which launched a single huge rocket; and Earth orbit rendezvous, where two or more launches of smaller rockets would place several parts of the lunar departure spacecraft which would be assembled in orbit. The former would require a huge Nova-class launcher and pads, while the latter would require several rockets to be launched in quick succession. Furthermore, the selection of the actual rockets was still ongoing; NASA was proposing the Nova design while their newly-acquired former Army group in Huntsville Alabama had proposed a series of slightly smaller designs known as Saturn.

This complicated the design of the launch complex, as it had to encompass two very different possibilities and rockets. Accordingly, early designs from 1961 show two sets of launch pads. The first was a series of three pads for Saturn along Playalinda Beach, with the southernmost near the current Eddy Creek Boat Launch, and the northernmost around Klondike Beach. Far to the south was a similar set of three pads for Nova, the southernmost just south of the Astronaut Beach House and the northern roughly at the location of the current Pad A.

The final selection of lunar orbit rendezvous and the Saturn V led to numerous changes. The Nova pads disappeared, and the three Saturn pads were moved southward. The southernmost was now at the current location of Pad A, while the northernmost was located between Patrol Road, the current boundary road for the LC39 site, and Playlandia Beach Road on the north. At the time, the original three were named from north to south: Pad A through Pad C. The pads were evenly spaced 8,700 feet (2,700 m) apart to avoid damage in the event of an explosion on a pad.

In March 1963, plans were formalized to build only two of the three pads; the northernmost was reserved for future expansion. The naming then changed to run south-to-north, such that B and C would be built as B and A respectively and the original 39A, if built, would become 39C. Some consideration for C's construction was made: the Crawlerway initially splits off from A toward B running north-northwest, and then bends north toward B a short distance north at Cochran Cove. Continuing straight would have led to C after a similar northward bend. The original construction of the Crawlerway included an interchange between B and the extension northward for C, which remains intact as of 2022, and the traffic-light warning system for the Crawlerway has lights for Pad C.

The plans still set aside room for the remaining two pads, now known as D and E. Pad D would have been built due west of Pad C, some distance inland along Patrol Road. Access to D would have branched off westward from the crawlerway at the point where C's crawlerway turned north. Pad E would have continued the line of pads along the coast, north of C near Playalinda Beach, close to the original location of the southernmost pad in the original layout. No diagram of the access to E can be found. Had all of them been built, C, D and E would have formed a triangle.

Months before a launch, the three stages of the Saturn V launch vehicle and the components of the Apollo spacecraft were brought inside the Vehicle Assembly Building (VAB) and assembled, in one of four bays, into a 363-foot (111 m)-tall space vehicle on one of three Mobile Launchers (ML). Each Mobile Launcher consisted of a two-story, 161-by-135-foot (49 by 41 m) launcher platform with four hold-down arms and a 446-foot (136 m) Launch Umbilical Tower (LUT) topped by a crane used to lift the spacecraft elements into position for assembly. The ML and unfueled vehicle together weighed 12,600,000 pounds (5,715 t).

The umbilical tower contained two elevators and nine retractable swing arms that were extended to the space vehicle—to provide access to each of the three rocket stages and the spacecraft for people, wiring, and plumbing—while the vehicle was on the launch pad and were swung away from the vehicle at launch. Technicians, engineers, and astronauts used the uppermost Spacecraft Access Arm to access the crew cabin. At the end of the arm, the white room provided an environmentally controlled and protected area for astronauts and their equipment before entering the spacecraft.

Early diagrams of the proposed layout also included the Nuclear Assembly Building, NAB, northeast of the VAB. These would be used to prepare the nuclear rocket engines being developed under the NERVA program, before moving them to the VAB for assembly into a rocket stack. This program was cancelled and the NAB was not built.

When the stack integration was completed, the Mobile Launcher was moved atop one of two crawler-transporters, or Missile Crawler Transporter Facilities, 3–4 miles (4.8–6.4 km) to its pad at a speed of 1 mile per hour (1.6 km/h). Each crawler weighed 6,000,000 pounds (2,720 t) and was capable of keeping the space vehicle and its launcher platform level while negotiating the 5 percent grade to the pad. At the pad, the ML was placed on six steel pedestals, plus four additional extensible columns.

After the ML was set in place, the crawler-transporter rolled a 410-foot (125 m), 10,490,000-pound (4,760 t) Mobile Service Structure (MSS) into place to provide further access for technicians to perform a detailed checkout of the vehicle, and to provide necessary umbilical connections to the pad. The MSS contained three elevators, two self-propelled platforms, and three fixed platforms. It was rolled back 6,900 feet (2,100 m) to a parking position shortly before launch.

While the ML was sat on its launch pedestals, one of two flame deflectors was slid on rails into place under it. Having two deflectors allowed for one to be used while the other was being refurbished after a previous launch. Each deflector measured 39 feet (12 m) high by 49 feet (15 m) wide by 75 feet (23 m) long, and weighed 1,400,000 pounds (635 t). During a launch, it deflected the launch vehicle's rocket exhaust flame into a trench measuring 43 feet (13 m) deep by 59 feet (18 m) wide by 449 feet (137 m) long.

The four-story Launch Control Center (LCC) was located 3.5 miles (5.6 km) away from Pad A, adjacent to the Vehicle Assembly Building, for safety. The third floor had four firing rooms (corresponding to the four bays in the VAB), each with 470 sets of control and monitoring equipment. The second floor contained telemetry, tracking, instrumentation, and data reduction computing equipment. The LCC was connected to the Mobile Launcher Platforms by a high-speed data link; and during launch a system of 62 closed-circuit television cameras transmitted to 100 monitor screens in the LCC.

Large cryogenic tanks located near the pads stored the liquid hydrogen and liquid oxygen (LOX) for the second and third stages of the Saturn V. The highly explosive nature of these chemicals required numerous safety measures at the launch complex. The pads were located 8,730 feet (2,660 m) away from each other. Before tanking operations began and during launch, non-essential personnel were excluded from the danger area.

Each pad had a 200-foot (61 m) evacuation tube running from the Mobile Launcher platform to a blast-resistant bunker 39 feet (12 m) underground, nicknamed Rubber room, equipped with survival supplies for 20 persons for 24 hours and reachable through a high-speed elevator.

A further Emergency Egress System was installed to allow fast escape of crew or technicians from pad in case of imminent catastrophic failure of the rocket. The system included seven baskets suspended from seven slidewires that extended from the fixed service structure to a landing zone 370 meters (1,200 ft) to the west. Each basket could hold up to three people, which slid down the wire reaching up to 80 kilometers per hour (50 mph), eventually reaching a gentle stop by means of a braking system catch net and drag chain which slowed and then halted the baskets.

Connections between the Launch Control Center, Mobile Launcher Platform, and space vehicle were made in the Pad Terminal Connection Room (PTCR), which was a two-story series of rooms located beneath the launch pad on the west side of the flame trench. The "room" was constructed of reinforced concrete and protected by up to 20 feet (6.1 m) of fill dirt.

The first launch from Launch Complex 39 came in 1967 with the first Saturn V launch, which carried the uncrewed Apollo 4 spacecraft. The second uncrewed launch, Apollo 6, also used Pad 39A. With the exception of Apollo 10, which used Pad 39B (due to the "all-up" testing resulting in a 2-month turnaround period), all crewed Apollo-Saturn V launches, commencing with Apollo 8, used Pad 39A.

A total of thirteen Saturn Vs were launched for Apollo, and the uncrewed launch of the Skylab space station in 1973. The mobile launchers were then modified for the shorter Saturn IB rockets, by adding a "milk-stool" extension platform to the launch pedestal, so that the S-IVB upper stage and Apollo spacecraft swing arms would reach their targets. These were used for three crewed Skylab flights and the Apollo-Soyuz Test Project, since the Saturn IB pads 34 and 37 at Cape Canaveral SFS had been decommissioned.

Space Shuttle

The thrust to allow the Space Shuttle to achieve orbit was provided by a combination of the Solid Rocket Boosters (SRBs) and the RS-25 engines. The SRBs used solid propellant, hence their name. The RS-25 engines used a combination of liquid hydrogen and liquid oxygen (LOX) from the external tank (ET), as the orbiter did not have room for internal fuel tanks. The SRBs arrived in segments via rail car from their manufacturing facility in Utah, the external tank arrived from its manufacturing facility in Louisiana by barge, and the orbiter waited in the Orbiter Processing Facility (OPF). The SRBs were first stacked in the VAB, then the External tank was mounted between them, and then, with the help of a massive crane, the orbiter was lowered and connected to the External tank.

The payload to be installed at the launch pad was independently transported in a payload transportation canister and then installed vertically at the Payload Changeout Room. Otherwise, payloads would have already been pre-installed at the Orbiter Processing Facility and transported within the orbiter's cargo bay.

The original structure of the pads was remodeled for the needs of the Space Shuttle, starting with Pad 39A after the last Saturn V launch, and, in 1977, that of Pad 39B after the Apollo-Soyuz in 1975. The first usage of the pad for the Space Shuttle came in 1979, when Enterprise was used to check the facilities prior to the first operational launch.

Each pads contained a two-piece access tower system, the Fixed Service Structure (FSS) and the Rotating Service Structure (RSS). The FSS permitted access to the Shuttle via a retractable arm and a "beanie cap" to capture vented LOX from the external tank.

A Sound Suppression Water System (SSWS) was added to protect the Space Shuttle and its payload from effects of the intense sound wave pressure generated by its engines. An elevated water tank on a 290-foot (88 m) tower near each pad stored 300,000 U.S. gallons (1,100,000 liters) of water, which was released onto the mobile launcher platform just before engine ignition. The water muffled the intense sound waves produced by the engines. Due to heating of the water, a large quantity of steam and water vapor was produced during launch.

The Gaseous Oxygen Vent Arm positioned a hood, often called the "Beanie Cap", over the top of the external tank (ET) nose cone during fueling. Heated gaseous nitrogen was used there to remove the extremely cold gaseous oxygen that normally vented out of the external tank. This prevented the formation of ice that could fall and damage the shuttle.

The Hydrogen Vent Line Access Arm mated the External Tank's Ground Umbilical Carrier Plate (GUCP) to the launch pad hydrogen vent line. The GUCP provided support for plumbing and cables, called umbilicals, that transferred fluids, gases, and electrical signals between two pieces of equipment. While the External Tank was being fueled, hazardous gas was vented from an internal hydrogen tank, through the GUCP, and out a vent line to a flare stack where it was burned off at a safe distance. Sensors at the GUCP measured gas level. The GUCP was redesigned after leaks created scrubs of STS-127 and were also detected during attempts to launch STS-119 and STS-133. The GUCP released from the ET at launch and fell away with a curtain of water sprayed across it for protection from flames.

In an emergency, the launch complex used a slidewire escape basket system for quick evacuation. Assisted by members of the closeout team, the crew would leave the orbiter and ride an emergency basket to the ground at speeds reaching up to 55 miles per hour (89 km/h). From there, the crew took shelter in a bunker. A modified M113 Armored Personnel Carrier could carry injured astronauts away from the complex to safety.

During the launch of Discovery on STS-124 on May 31, 2008, the pad at LC-39A suffered extensive damage, in particular to the concrete trench used to deflect the SRB's flames. The subsequent investigation found that the damage was the result of carbonation of epoxy and corrosion of steel anchors that held the refractory bricks in the trench in place. The damage had been exacerbated by the fact that hydrochloric acid is an exhaust by-product of the solid rocket boosters.

After the launch of Skylab in 1973, Pad 39A was reconfigured for the Space Shuttle, with shuttle launches beginning with STS-1 in 1981, flown by the Space Shuttle Columbia. After Apollo 10, Pad 39B was kept as a backup launch facility in the case of the destruction of 39A, but saw active service during all three Skylab missions, the Apollo-Soyuz test flight, and a contingency Skylab Rescue flight that never became necessary. After the Apollo-Soyuz Test Project, 39B was reconfigured similarly to 39A; but due to additional modifications (mainly to allow the facility to service a modified Centaur-G upper stage), along with budgetary restraints, it was not ready until 1986. The first shuttle flight to use it was STS-51-L, which ended with the Challenger disaster, after which the first return-to-flight mission, STS-26, was launched from 39B.

Just as for the first 24 shuttle flights, LC-39A supported the final shuttle flights, starting with STS-117 in June 2007 and ending with the retirement of the Shuttle fleet in July 2011. Prior to the SpaceX lease agreement, the pad remained as it was when Atlantis launched on the final shuttle mission on July 8, 2011, complete with a mobile launcher platform.

With the retirement of the Space Shuttle in 2011, and the cancellation of Constellation Program in 2010, the future of the Launch Complex 39 pads was uncertain. By early 2011, NASA began informal discussions on use of the pads and facilities by private companies to fly missions for the commercial space market, culminating in a 20-year lease agreement with SpaceX for Pad 39A.

Talks for use of the pad were underway between NASA and Space Florida—the State of Florida's economic development agency—as early as 2011, but no deal materialized by 2012, and NASA then pursued other options for removing the pad from the federal government inventory.

Constellation program

The last Shuttle launch from pad 39B was the nighttime launch of STS-116 on December 9, 2006. To support the final Shuttle mission to the Hubble Space Telescope STS-125 launched from pad 39A in May 2009, Endeavour was placed on 39B if needed to launch the STS-400 rescue mission.

After the completion of STS-125, 39B was converted to launch the single test flight of the Constellation Program Ares I-X on October 28, 2009. This program was later canceled.

SpaceX

By early 2013, NASA publicly announced that it would allow commercial launch providers to lease LC-39A, and followed that, in May 2013, with a formal solicitation for proposals for commercial use of the pad. There were two competing bids for the commercial use of the launch complex. SpaceX submitted a bid for exclusive use of the launch complex, while Jeff Bezos' Blue Origin submitted a bid for shared non-exclusive use of the complex, so that the launchpad would handle multiple vehicles, and costs could be shared over the long-term. One potential shared user in the Blue Origin plan was United Launch Alliance. Prior to the end of the bid period, and prior to any public announcement by NASA of the results of the process, Blue Origin filed a protest with the U.S. General Accounting Office (GAO) "over what it says is a plan by NASA to award an exclusive commercial lease to SpaceX for use of mothballed space shuttle launch pad 39A." NASA had planned to complete the bid award and have the pad transferred by October 1, 2013, but the protest "will delay any decision until the GAO reaches a decision, expected by mid-December." On December 12, 2013, the GAO denied the protest and sided with NASA, which argued that the solicitation contained no preference on the use of the facility as multi-use or single-use. "The document merely asks bidders to explain their reasons for selecting one approach instead of the other and how they would manage the facility."

On April 14, 2014, the privately owned launch service provider SpaceX signed a 20-year lease for Launch Complex 39A (LC-39A). The pad was modified to support launches of both Falcon 9 and Falcon Heavy launch vehicles, modifications that included the construction of a large Horizontal Integration Facility (HIF) similar to that used at existing SpaceX-leased facilities at Cape Canaveral Space Force Station and Vandenberg Air Force Base, horizontal integration being markedly difference from the vertical integration process used to assemble NASA's Apollo and Space Shuttle vehicles at the launch complex. Additionally, new instrumentation and control systems were installed, and substantial new plumbing was added for a variety of rocket liquids and gases.

In 2015, SpaceX built the Horizontal Integration Facility just outside the perimeter of the existing launch pad in order to house both the Falcon 9 and the Falcon Heavy rockets, and their associated hardware and payloads, during preparation for flight. Both types of launch vehicles will be transported from the HIF to the launch pad aboard a Transporter Erector (TE) which will ride on rails up the former crawlerway path. Also in 2015, the launch mount for the Falcon Heavy was constructed on Pad 39A over the existing infrastructure. The work on both the HIF building and the pad was substantially complete by late 2015. A rollout test of the new Transporter Erector was conducted in November 2015.

In February 2016, SpaceX indicated that they had "completed and activated Launch Complex 39A", but still had more work yet to do to support crewed flights. SpaceX originally planned to be ready to accomplish the first launch at pad 39A—of a Falcon Heavy—as early as 2015, as they had had architects and engineers working on the new design and modifications since 2013. By late 2014, a preliminary date for a wet dress rehearsal of the Falcon Heavy was set for no earlier than July 1, 2015. Due to a failure in a June 2015 Falcon 9 launch, SpaceX had to delay launching the Falcon Heavy in order to focus on the Falcon 9's failure investigation and its return to flight. In early 2016, considering the busy Falcon 9 launch manifest, it became unclear if the Falcon Heavy would be the first vehicle to launch from Pad 39A, or if one or more Falcon 9 missions would precede a Falcon Heavy launch. In the following months, the Falcon Heavy launch was delayed multiple times and eventually pushed back to February 2018.

In 2018, SpaceX made further modifications to LC 39A to prepare it to accommodate the manned Dragon 2. These modifications included installing a new crew access arm, refurbishing the emergency egress slidewire system, and raising it up to the level of the new arm. The LC 39A fixed service structure was also repainted during this work.

In 2019, SpaceX began substantial modification to LC 39A in order to begin work on phase 1 of the construction to prepare the facility to launch prototypes of the large 9 m (30 ft)-diameter methalox reusable rocket—Starship—from a launch stand, which will fly from 39A on suborbital test flight trajectories with six or fewer Raptor engines. A second phase of the construction is planned for 2020 to build a much more capable launch mount capable of launching the entire Starship launch vehicle, powered by 43 Raptor engines and producing a total of 72 MN (16,000,000 lbf) liftoff thrust when departing 39A.

The first SpaceX launch from pad 39A was SpaceX CRS-10 on February 19, 2017, using a Falcon 9 launch vehicle; it was the company's 10th cargo resupply mission to the International Space Station, and the first uncrewed launch from 39A since Skylab.

While Cape Canaveral's Space Launch Complex 40 (SLC-40) was undergoing reconstruction after the loss of the AMOS-6 satellite on September 1, 2016, all SpaceX's east coast launches were from Pad 39A until SLC-40 became operational again in December 2017. These included the May 1, 2017, launch of NROL-76, the first SpaceX mission for the National Reconnaissance Office, with a classified payload.

On February 6, 2018, Pad 39A hosted the successful liftoff of the Falcon Heavy on its maiden launch, carrying Elon Musk's Tesla Roadster car to space; and the first flight of the human-rated spacecraft Crew Dragon (Dragon 2) took place there on March 2, 2019.

The second Falcon Heavy flight, carrying the Arabsat-6A communications satellite for Arabsat of Saudi Arabia, successfully launched on April 11, 2019. The satellite is to provide Ku band and Ka band communication services for the Middle East and northern Africa, as well as for South Africa. The launch was notable as it marked the first time that SpaceX was able to successfully soft-land all three of the reusable booster stages, which will be refurbished for future launches.

The SpaceX Demo-2 − the first crewed test flight of the Crew Dragon "Endeavour" spacecraft, with astronauts Bob Behnken and Doug Hurley on board launched from Complex 39A on May 30, 2020 and docked to Pressurized Mating Adapter 2 on the Harmony module of the ISS on May 31, 2020.

Launch statistics

Pad 39A launches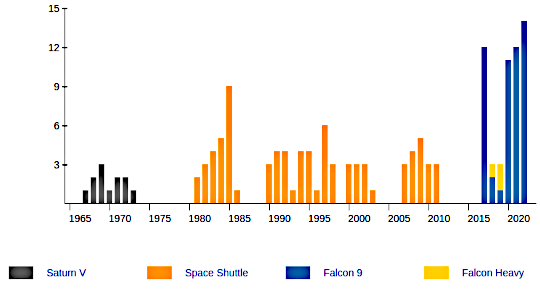

Pad 39B launches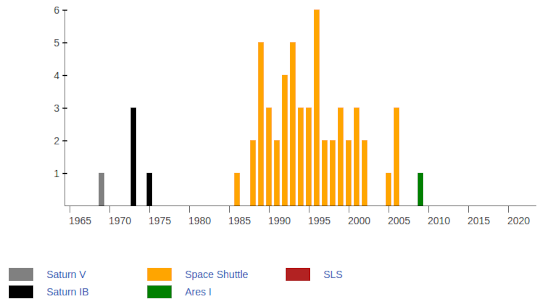

Current status

Launch Complex 39A

SpaceX has launched their launch vehicles from Launch Complex 39A and built a new hangar nearby.

SpaceX assembles its launch vehicles horizontally in a hangar near the pad, and transports them horizontally to the pad before erecting the vehicle to vertical for the launch. For military missions from Pad 39A, payloads will be vertically integrated, as that is required per launch contract with the U.S. Space Force.

Pad 39A is used to host launches of astronauts on the Crew Dragon capsule in a public–private partnership with NASA. In August 2018, SpaceX's Crew Access Arm (CAA) was installed on a new level, which was built at the necessary height to enter the Crew Dragon spacecraft atop a Falcon 9 rocket.

Launch Complex 39B

Since the Ares I-X test flight in 2009, Launch Complex 39B is being reconfigured for use by NASA's Space Launch System rocket, a Shuttle-derived launch vehicle which will be used in the Artemis program and subsequent Moon to Mars campaigns. The pad has also been leased for use by NASA to aerospace company Northrop Grumman, for use as a launch site for their Shuttle-derived OmegA launch vehicle, for National Security Space Launch flights and commercial launches.

Launch Complex 39C

Launch Complex 39C is a new facility for small-lift launch vehicles. It was built in 2015 within the Launch Complex 39B perimeter. It was to serve as a multi-purpose site that allowed companies to test the vehicles and capabilities of the smaller class of rockets, making it more affordable for smaller companies to break into the commercial spaceflight market. However, its primary customer Rocket Lab opted to launch their Electron rocket from Wallops Island, instead. Several small-lift launch-vehicle companies also wanted to launch their rockets from a dedicated site at Cape Canaveral instead of 39C.

Construction of the pad began in January 2015 and was completed in June 2015. Kennedy Space Center director Robert D. Cabana and representatives from the Ground Systems Development and Operations (GSDO) Program and the Center Planning and Development (CPD) and Engineering directorates marked the completion of the new pad during a ribbon-cutting ceremony on July 17, 2015. "As America's premier spaceport, we're always looking for new and innovative ways to meet America's launch needs, and one area that was missing was small class payloads", Cabana said.

The concrete pad measures about 50 feet (15 m) wide by about 100 feet (30 m) long and could support the combined weight of a fueled launch vehicle, payload, and customer-provided launch mount up to about 132,000 pounds (60,000 kg), and an umbilical tower structure, fluid lines, cables, and umbilical arms weighing up to about 47,000 pounds (21,000 kg). There is a universal propellant servicing system to provide liquid oxygen and liquid methane fueling capabilities for a variety of small-class rockets.

With the addition of Launch Complex 39C, KSC offered the following processing and launching features for companies working with small-class vehicles (maximum thrust up to 200,000 lbf or 890 kN):

Future development

Previous Kennedy Space Center (KSC) Master Plan recommendations—in 1966, 1972, and 1977—noted that an expansion of KSC's vertical launch capacity could occur when the market demand existed. The 2007 Site Evaluation Study recommended an additional vertical launch pad, Launch Complex 49 (LC-49), to be sited north of existing LC-39B.

As part of the Environmental Impact Study (EIS) process, this proposed launch complex was consolidated from two pads (designated in the 1963 plans as 39C and 39D) to one that would provide greater separation from LC-39B. The area was expanded to accommodate a wider variety of launch azimuths, helping to protect against potential overflight concerns of LC-39B. This LC-49 launch facility could accommodate medium to large launch vehicles.

The 2007 Vertical Launch Site Evaluation Study concluded that a vertical launch pad could also be sited to the south of 39A, and to the north of pad 41, to accommodate small to medium launch vehicles. Designated as Launch Complex 48 (LC-48), this area is best suited to accommodate small to medium class launch vehicles, due to its closer proximity to LC-39A and LC-41. Due to the nature of these activities, required quantity-distance arcs, launch hazard impact limit lines, other safety setbacks, and exposure limits will be specified for safe operations. Details of the proposed launch pads were published in the Kennedy Space Center Master Plan in 2012.

The Master Plan also notes a proposed New Vertical Launchpad northwest of LC-39B and a Horizontal Launch Area north of the LC-49 and converting the Shuttle Landing Facility (SLF) and its apron areas into a second Horizontal Launch Area.

Space Florida has proposed that Launch Complex 48 be developed for use by Boeing's Phantom Express and that three landing pads be built for reusable booster systems, to provide more landing options for SpaceX's Falcon 9 and Falcon Heavy, Blue Origin's New Glenn, and other potential reusable vehicles. The pads would be located east of the Horizontal Launch Area and north of LC-39B

In August 2019, SpaceX submitted an Environmental Assessment for Starship launch system at Kennedy Space Center. This document included plans for the construction of additional structures at LC-39A to support Starship launches, including a dedicated pad, liquid methane tanks, and a Landing Zone. These are separate from the existing structures that support Falcon 9 and Falcon Heavy launches.