Terminology and notation

In 1806, Jean-Robert Argand introduced the term module, meaning unit of measure in French, specifically for the complexabsolute value, and it was borrowed into English in 1866 as the Latin equivalent modulus. The term absolute value has been used in this sense from at least 1806 in French and 1857 in English. The notation |x|, with a vertical bar on each side, was introduced by Karl Weierstrass in 1841. Other names for absolute value include numerical value and magnitude. In programming languages and computational software packages, the absolute value of x is generally represented by abs(x), or a similar expression.

The vertical bar notation also appears in a number of other mathematical contexts: for example, when applied to a set, it denotes its cardinality; when applied to a matrix, it denotes its determinant. Vertical bars denote the absolute value only for algebraic objects for which the notion of an absolute value is defined, notably an element of a normed division algebra, for example a real number, a complex number, or a quaternion. A closely related but distinct notation is the use of vertical bars for either the euclidean norm or sup norm of a vector in , although double vertical bars with subscripts (, respectively) are a more common and less ambiguous notation.

Definition and properties

Real numbers

For any real number x, the absolute value or modulus of x is denoted by |x| (a vertical bar on each side of the quantity) and is defined as

The absolute value of x is thus always either positive or zero, but never negative: when x itself is negative (x < 0), then its absolute value is necessarily positive (|x| = −x > 0).

From an analytic geometry point of view, the absolute value of a real number is that number’s distance from zero along the real number line, and more generally the absolute value of the difference of two real numbers is the distance between them. Indeed, the notion of an abstract distance function in mathematics can be seen to be a generalisation of the absolute value of the difference (see «Distance» below).

Since the square root symbol represents the unique positive square root (when applied to a positive number), it follows that

is equivalent to the definition above, and may be used as an alternative definition of the absolute value of real numbers.

The absolute value has the following four fundamental properties (a, b are real numbers), that are used for generalization of this notion to other domains:

	Non-negativity
	Positive-definiteness
	Multiplicativity
	Subadditivity, specifically the triangle inequality

Non-negativity, positive definiteness, and multiplicativity are readily apparent from the definition. To see that subadditivity holds, first note that one of the two alternatives of taking s as either –1 or +1 guarantees that Now, since and , it follows that, whichever is the value of s, one has for all real . Consequently, , as desired. (For a generalization of this argument to complex numbers, see «Proof of the triangle inequality for complex numbers» below.)

Some additional useful properties are given below. These are either immediate consequences of the definition or implied by the four fundamental properties above.

	Idempotence (the absolute value of the absolute value is the absolute value)
	Evenness (reflection symmetry of the graph)
	Identity of indiscernibles (equivalent to positive-definiteness)
	Triangle inequality (equivalent to subadditivity)
	Preservation of division (equivalent to multiplicativity)
	Reverse triangle inequality (equivalent to subadditivity)

Two other useful properties concerning inequalities are:

These relations may be used to solve inequalities involving absolute values. For example:

The absolute value, as «distance from zero», is used to define the absolute difference between arbitrary real numbers, the standard metric on the real numbers.

Complex numbers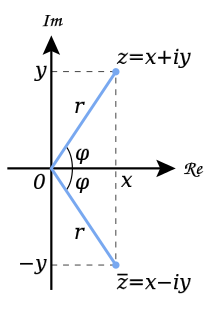

The absolute value of a complex number z is the distance r of z from the origin. It is also seen in the picture that z and its complex conjugate have the same absolute value.

Since the complex numbers are not ordered, the definition given at the top for the real absolute value cannot be directly applied to complex numbers. However, the geometric interpretation of the absolute value of a real number as its distance from 0 can be generalised. The absolute value of a complex number is defined by the Euclidean distance of its corresponding point in the complex plane from the origin. This can be computed using the Pythagorean theorem: for any complex number

where x and y are real numbers, the absolute value or modulus of z is denoted |z| and is defined by

where Re(z) = x and Im(z) = y denote the real and imaginary parts of z, respectively. When the imaginary part y is zero, this coincides with the definition of the absolute value of the real number x.

When a complex number z is expressed in its polar form as

with is the argument (or phase) of z), its absolute value is

Since the product of any complex number z and its complex conjugate with the same absolute value, is always the non-negative real number the absolute value of a complex number can be conveniently expressed as

resembling the alternative definition for reals:

The complex absolute value shares the four fundamental properties given above for the real absolute value.

In the language of group theory, the multiplicative property may be rephrased as follows: the absolute value is a group homomorphism from the multiplicative group of the complex numbers onto the group under multiplication of positive real numbers.

Importantly, the property of subadditivity («triangle inequality») extends to any finite collection of n complex numbers as

This inequality also applies to infinite families, provided that the infinite series is absolutely convergent. If Lebesgue integration is viewed as the continuous analog of summation, then this inequality is analogously obeyed by complex-valued, measurable functions when integrated over a measurable subset E:

(This includes Riemann-integrable functions over a bounded interval [a, b] as a special case.)

Proof of the complex triangle inequality

The triangle inequality, as given by (*), can be demonstrated by applying three easily verified properties of the complex numbers: Namely, for every complex number

(i): there exists

(ii):

Also, for a family of complex numbers In particular,

(iii): if

Proof of (*): Choose (summed over ). The following computation then affords the desired inequality:

It is clear from this proof that equality holds in (*) exactly if all the are non-negative real numbers, which in turn occurs exactly if all nonzero have the same argument, i.e., for a complex constant and real constants

Since measurable implies that is also measurable, the proof of the inequality (**) proceeds via the same technique, by replacing with

Absolute value function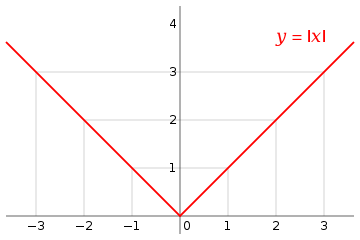

The graph of the absolute value function for real numbers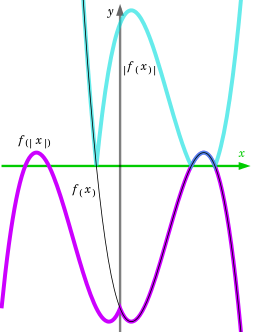

Composition of absolute value with a cubic function in different orders

The real absolute value function is continuous everywhere. It is differentiable everywhere except for x = 0. It is monotonically decreasing on the interval (−∞,0] and monotonically increasing on the interval [0,+∞). Since a real number and its opposite have the same absolute value, it is an even function, and is hence not invertible. The real absolute value function is a piecewise linear, convex function.

Both the real and complex functions are idempotent.

Relationship to the sign function

The absolute value function of a real number returns its value irrespective of its sign, whereas the sign (or signum) function returns a number’s sign irrespective of its value. The following equations show the relationship between these two functions:

or

and for x ≠ 0,

Derivative

The real absolute value function has a derivative for every x ≠ 0, but is not differentiable at x = 0. Its derivative for x ≠ 0is given by the step function:

The subdifferential of |x| at x = 0 is the interval [−1,1].

The complex absolute value function is continuous everywhere but complex differentiable nowhere because it violates the Cauchy–Riemann equations.

The second derivative of |x| with respect to x is zero everywhere except zero, where it does not exist. As a generalised function, the second derivative may be taken as two times the Dirac delta function.

Antiderivative

The antiderivative (indefinite integral) of the real absolute value function is

where C is an arbitrary constant of integration. This is not a complex antiderivative because complex antiderivatives can only exist for complex-differentiable (holomorphic) functions, which the complex absolute value function is not.

Distance

The standard Euclidean distance between two points

and

in Euclidean n-space is defined as:

This can be seen as a generalisation, since for a₁ and b₁ real, i.e. in a 1-space, according to the alternative definition of the absolute value,

and for complex numbers, i.e. in a 2-space,

The above shows that the «absolute value»-distance, for real and complex numbers, agrees with the standard Euclidean distance, which they inherit as a result of considering them as one and two-dimensional Euclidean spaces, respectively.

The properties of the absolute value of the difference of two real or complex numbers: non-negativity, identity of indiscernibles, symmetry and the triangle inequality given above, can be seen to motivate the more general notion of a distance function as follows:

A real valued function d on a set X × X is called a metric (or a distance function) on X, if it satisfies the following four axioms:

	Non-negativity
	Identity of indiscernibles
	Symmetry
	Triangle inequality

Generalizations

Ordered rings

The definition of absolute value given for real numbers above can be extended to any ordered ring. That is, if a is an element of an ordered ring R, then the absolute value of a, denoted by |a|, is defined to be:

where −a is the additive inverse of a, 0 is the additive identity element, and < and ≥ have the usual meaning with respect to the ordering in the ring.

Fields

A real-valued function v on a field F is called an absolute value (also a modulus, magnitude, value, or valuation) if it satisfies the following four axioms:

	Non-negativity
	Positive-definiteness
	Multiplicativity
	Subadditivity or the triangle inequality

Where 0 denotes the additive identity element of F. It follows from positive-definiteness and multiplicativity that v(1) = 1, where 1 denotes the multiplicative identityelement of F. The real and complex absolute values defined above are examples of absolute values for an arbitrary field.

If v is an absolute value on F, then the function d on F × F, defined by d(a, b) = v(a − b), is a metric and the following are equivalent:

• d satisfies the ultrametric inequality for all x, y, z in F.
• is bounded in R.
• 
• 
• 

An absolute value which satisfies any (hence all) of the above conditions is said to be non-Archimedean, otherwise it is said to be Archimedean.

Vector spaces

A real-valued function on a vector space V over a field F, represented as ‖·‖, is called an absolute value, but more usually a norm, if it satisfies the following axioms:

For all a in F, and v, u in V,

	Non-negativity
	Positive-definiteness
	Positive homogeneity or positive scalability
	Subadditivity or the triangle inequality

The norm of a vector is also called its length or magnitude.

In the case of Euclidean space Rⁿ, the function defined by

is a norm called the Euclidean norm. When the real numbers R are considered as the one-dimensional vector space R¹, the absolute value is a norm, and is the p-norm (see L^p space) for any p. In fact the absolute value is the «only» norm on R¹, in the sense that, for every norm ‖·‖ on R¹, ‖x‖ = ‖1‖ ⋅ |x|. The complex absolute value is a special case of the norm in an inner product space. It is identical to the Euclidean norm, if the complex plane is identified with the Euclidean plane R².

Composition algebras

The real numbers ℝ, complex numbers ℂ, and quaternions ℍ are all composition algebras with norms given by definite quadratic forms. The absolute value in these division algebras is given by the square root of the composition algebra norm.

In general the norm of a composition algebra may be a quadratic form that is not definite and has null vectors. However, as in the case of division algebras, when an element x has a non-zero norm, then x has a multiplicative inverse given by x*/N(x).

Text from Wikipedia is available under the Creative Commons Attribution/Share-Alike License; additional terms may apply.

Published in May 2019.

Click here to read more articles related to aviation and space!